加权几何平均数

出处：按学科分类—经济 山东人民出版社《简明经济百科辞典》第476页（860字）

当计算几何平均数每个变量值的次数不相同时应用加权几何平均数。

公式为：

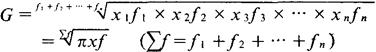
式中：

∑f代表次数(或权数)总和；

f代表每个变量值的次数(或权数)。

此公式采用对数计算，则为：

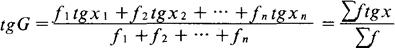
例如，投资银行某笔投资的年利率是按复利计算的，25年的年利率是：有1年为3%，4年为4%，8年为8%，10年为10%，2年为15%，求平均年利率。

计算平均年利率须将各年利率加100%换算为各年本利率后，再按加权几何平均数计算平均年本利率，再减100%得平均年利率。

列表计算如下：

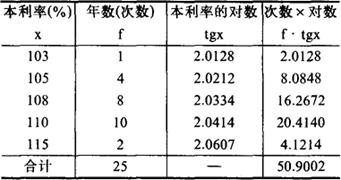
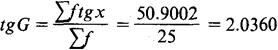
查反对数得：G=108．6%。

银行该笔投资，25年的年平均本利率为108．6%，年平均率即为8．6%(108．6%－100%)。

平均数计算方法的选择应根据社会经济现象的客观性质和研究目的而定，几何平均数方法不应用其他平均数方法。

从计算结果上比较是：几何平均数大于调和平均数而小于算术平均数，只有当所有变量值都相同的情况下，三种平均数才相等。它们的关系用不等式表示是：H≤G≤X

由这个不等式的关系可以判断：在该用算术平均数的场合而用了其他平均数则结果偏小，在该用调和平均数的场合而用了其他平均数则结果偏大，在该用几何平均数的时候用了调和平均数结果偏小，用了算术平均数则结果偏大。