知道逻辑

出处：按学科分类—自然科学总论 山东人民出版社《方法大辞典》第75页（1687字）

属于认识论逻辑的范围，研究含有知道、认可等认知模态词的命题及其推理的逻辑学科。

不过，它所研究的“知道”是指知道的命题意义，即知道这件事或那件事怎么样，而不是指知道这件事或那件事怎么做。它的目的是在研究知道命题关系的基础上建立知道模态逻辑系统。

在知道逻辑中，知道和认可都被处理为二项关系，前者用K表示，后者用A表示，并且用x，y，z，……，表示认知的主体，用p，q，r，……，表示认知的命题或观点。于是知道命题和认可命题就可表示为：

K(x，p)：x知道p真；

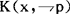：x知道p假；

A(x，p)：x认可p真；

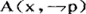：x认可p假。

在日常推理中，当我们并不确知p假时，我们会认可p真，反过来，我们认可p真，也就是并不确知p假；同理，当我们确知p真时，我们将不认可非p，反之亦然。因此我们有下述等值式：

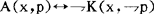(1)

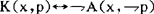(2)

对于p真和p假，任何人都至少认可其中之一，即

(3)

并且，在日常推理中还有

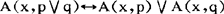(4)

p→A(x，p)5)

(5)是说，若p真，则x认可p。

可以看出，模态词知道(K)与必然(□)、认可(A)与可能(◇)地位大致相同，因而可以用规定“必然”与“可能”的语义的方法来规定“知道”与“认可”的语义，甚至可以用上述(1)一(5)作为公理，建立一个关于知道的模态系统，它在形式上应与关于“必然”“可能”的模态逻辑系统有一致的地方，两者有许多公理和推理规则是平行的。

但是，由于知道逻辑引进的认知主体，所以内容要丰富得多。

若主体是一位全知者G，则他只认可事实，于是就有

A(G，p)→p (6)

根据上述(1)，则有：

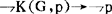(7)

(7)假言易位，则有：

p→K(G，p) (8)

由于G知道p蕴涵p，即

K(G，p)→p (9)

于是就有：

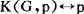
这就是说，G的知道逻辑就是普通的命题逻辑。

反之，若主体是全无知者O，即他只知道逻辑必然的东西，而对具体事实一无所知，即：

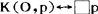
这就是说，O的知道逻辑就是真值模态逻辑。可以看出，知道逻辑通过许多中间情况与命题逻辑、真值模态逻辑连接起来了，当然，这种联事是错综复杂的。

知道逻辑有待进一步研究。

它对于认识论和人工智能研究有重要意义。