模型

出处：按学科分类—自然科学总论 山东人民出版社《方法大辞典》第103页（1215字）

模型论是研究形式系统及其模型之间关系的数学分支。

这里我们介绍模型的概念。

为简单起见，我们这里只考虑一阶理论的模型。

设L是一个一阶形式语言(参见“形式语言”)，L的i元谓词符号和函数符号分别是和(i≥1，n=1，2，…)，L的常元符号为C_i(i=1，2，…)。

L的模型m是一个二元偶(M，φ)，其中M是一个非空集，φ是满足下列条件的函数

(1)若Rⁱ是L的i元谓词符号，则；

(2)若Fⁱ是L的i元函数符号，则φ(Fⁱ)是由Mⁱ到M的函数；

(3)若C是L的常元符号，则φ(c)εM。

我们下面常以X^m表示φ(x)。

语言L的模型m的一个指派是指由L的变元的集合到M中的一个函数。

设m是语言L的模型，t是L的一个项，定义t在m中的解释t^m如下：

(1)如果t是一个常元符号c，则对于所有指派s，t^m(s)=C^m；

(2)如果t是L中的一个变元V，则对于所有指派S，t^m(S)=S(V)；

(3)如果t是项f(t1，…tn)，则对于所有指派s，定义

现在，我们给出一公式φ在指派S下在模型m中真的定义(用符号表示为)。

(1) 当且仅当；

(2)当且仅当εRm

(3)当且仅当不成立；

(4)当且仅当并且；

(5)当且仅当或者；

(6)当且仅当要么不成立，要么；

(7)当且仅当存在aεM，使得

(8)当且仅当对于所有的aεM，

当φ是一个语句时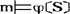，当指派S无关。

如果存在一个指派S(因此对于所有指派)成立，则称φ在m中真，或称m是φ的模型。

如果Φ是一个理论(即一个语句集)，当Φ中每个语句均在m中真时，称m是Φ的模型。