主成分分析法
出处：按学科分类—自然科学总论 山东人民出版社《方法大辞典》第171页（797字）
多元分析的一个重要问题是用少数几个指标来表示多个变量的变动。
主成分分析法是处理这种问题的一个方法，其用意在于重新组织数据后使变量的维数显着降低，而信息损失尽可能少，以便在低维子空间上顺利研究有关问题，办法是用原变量的线性组合作为新变量，并从中选出若干方差较大的，且互不相关的以代替原变量。假定Xpx1是P维随机向量，EX=μ，Varx=∑，现求x的线性函数a’x使得a’x的方差尽可能的大，由于var(a’x)=a’∑a，对任给的常数C，var(ca’x=c2a’∑a，因此对a不加限制时，问题就会变成没有什么意义了，可限制a’a=1求var(a’x)的最大值。实际上，就是求
的值。用Lagange乘子法或矩阵的特征根的求法可以知道，这个值就是矩阵∑的最大特征根λ1，并且a就是λ1相应的特征向量。
利用非负定阵∑的谱分解，设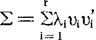
，r=rk(∑)，λ1≥λ2≥…≥λr是∑的全部非零特征根，υi是λi的相应特征向量，于是
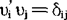，且
，i，j=1，2，…r。由此可知，选ai=γi，i=1，…，r，则有a’ai=1，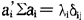
，
。
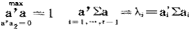我们把∑的非零特征根λ1≥…≥λτ所相应的标准化特征向量
分别作为系数向量，a’x，…，a’rx分别称为随机向量X的第一主成分，第二主成分，第r主成分。主成分的统计意义是把P个随机变量的总方差tr∑分解为r个不相关的随机变量的方差之和λ1+…+λr，使第一主成分的方差达到最大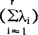
表明了λ1在全部方差中的比值，称为第一主成分的贡献率。
这个值越大，表明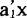
这个变量“综合”X1，……，XP的能力越强。
现在就可以明白为什么主成分的次序是按特征根λ1，……，λr取值的大小顺序排列的。
通常不需要用全部的主成分，只用其中前面的几个。一般的原则是，当(λ1+…+λ1)／tr∑≥85%时，采用前L个就足够了，因为这L个主成分的方差已占全部的总方差的85%以上。