抽屉原理

出处：按学科分类—自然科学总论 山东人民出版社《方法大辞典》第213页（423字）

又叫鸽舍原理。

为了纪念19世纪德国数学家狄利克利，抽屉原理也叫狄利克利原理，这个原理最简单的表达方式是：假如有n+1个(或更多)物体装入n个盒子里，那么一定有某个盒子至少装有两个物体。

抽屉原理在数论和组合论中有许多重要的应用，以下便是应用抽屉原理得到的几个重要结果：(1)若1≤a₁2<…n+1≤2n，则有l≤ii｜a_j，这是因为每一个a_i都可以写成2^λib_i，λ_i≥0，2xb_i(i=1，2，…，n+1)，其中b_i<2n，由于在1，2，…，2n中恰有n个不同的奇数，故在b₁，b₂，…，b_n+1中应用抽屉原理，则至少有两个相同，设b_i=b_j，1≤i≤j≤n+1，于是便有a_i｜a_j。这一重要结果是在1935年由爱多士提出，并由莱梅证明的。(2)设a₁，a₂，…a_n是数1，2，…，n的某种排列，2xn，则乘积(a₁－1)(a₂－2)…(a_n－n)是偶数；(3)设1≤m≤n，联立方程组

L₁=a_i1x₁+…+a_1nx_n=0

L₂=a₂₄xj+…+a_2nx_n=0， (A)

…………………………

L_m=a_m1x₁+…+a_mnx_n=0，

其中a_jk(j=1，2，…，m，k=1，2，…，n)为整数，如果X₁…，x_n是(A)的一组解，记为向量形式X=(x₁，…，x_n)，X称为(A)的一个解向量，则(A)存在解向量X=(x₁，…，x_n)≠0，且满足

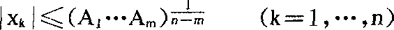
其中A_j=｜a_j1｜+｜a_j2+…+｜a_jn (j=1，…，n)

在用有理数去逼近无理数的问题中，抽屉原理也有重要应用：对给定的无理数θ，选择有理整数x＞0，y，使得｜θ－y／x｜的界比起分母x来要求尽可能地小，由抽屉原理可知，对于任给的整数N＞0，使得｜θ－y／x｜<1／(xN)成立的x≤n，y总是存在的，因此，若设｜θ－y／x｜<1／Mx²具有无限多对有理整数解x，y的正数M的最小上界为M(θ)，那么，由此即可推知：对任何无理数θ，有1≤M(θ)≤∞，这就是丢番图逼近论中关于M(θ)的一个重要结果。

这一结果在逼近论等许多问题中都得到了重要应用。