数论变换

出处：按学科分类—自然科学总论 山东人民出版社《方法大辞典》第280页（849字）

研究数论函数的性质及数论函数之间关系的重要方法。

在筛法等问题中有许多重要应用。最重要的数论变换是狄里克利乘积。

设f(n)与g(n)是两个数论函数，则称为f(n)与g(n)的狄里克利乘积或卷积，记作h=f*g。

例如，设u(n)≡1，n≥1；1(1)=1，n＞1时，I(n)=0；μ(n)为茂陛乌斯函数，即当n=1时，μ(n)=1，当n=p₁p₂…p_s，(p₁2<…s)时μ(n)=(－1)^s，对其它的n，μ(n)=0，则有I=μ*u，亦即当n=1时为1，当n＞1时为0，所以单位函数I(n)是茂陛乌斯函数与u(n)的狄里克利乘积、狄里克利乘积的一个重要性质是它满足结合律和交换律，亦即，若f，g，h为任意三个数论函数，则f*g==g*f，(f*g)*h=f*(g*h)，狄里克利乘积作为数论函数之间的一种重要运算，其逆运算同样也是十分重要的，其中最重要的就是所谓狄里克利逆。

设f(n)为数论函数，若存在一个数论函数g(n)，使得f*g=I，则称g(n)为f(n)的狄里克利逆，并记g(n)=f1－1(n)，例如，由于μ*u=1，所以μ(n)的逆为u(n)≡1，u(n)的逆则为μ(n)。

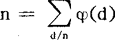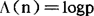狄里克利乘积中，应用最广泛的是它的特例，即茂陛乌斯变换，若F=f*u，即，则称F为f的茂陛乌斯变换，例如，I(n)就是μ(n)的茂陛乌斯变换；除数函数则是u(n)的茂陛乌斯变换；恒等函数e(n)=n，n≥1就是欧拉函数φ(n)的茂陛乌斯变换，亦即；若为蒙哥尔特函数，即当n=p^k，k≥1时,，对其它的n，，则logn为的茂陛乌斯变换，亦即，茂陛乌斯变换的一个重要性质是：若F=f*u，则f=F*μ，亦即若，则有，由此便可得到及等重要公式，茂陛乌斯变换的另一个重要性质是：f(n)的茂陛乌斯变换F(n)为可乘函数的充分必要条件是f(n)为可乘函数，因此，当f(n)为可乘时，就有，由此便立即可以得到，以及等重要公式。