线性规划图解法
书籍:中国物资管理辞典
出处:按学科分类—经济 中国财政经济出版社《中国物资管理辞典》第493页(782字)
用几何作图法求解只含两个或三个变量的线性规划问题的方法。
基本思路是先由约束条件确定可行域,再根据目标函数在可行域中寻找最优解。
设有线性规划问题。求x1、x2满足约束条件:
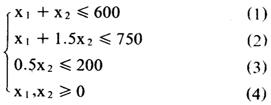
使目标函数达到:
Max Z=30x1+40x2 (5)
图解步骤如下:(1)确定可行域。
以x1为横轴,x2为纵轴,x1≥0,x2≥0限制可行解区域为包括坐标轴在内的第一象限。
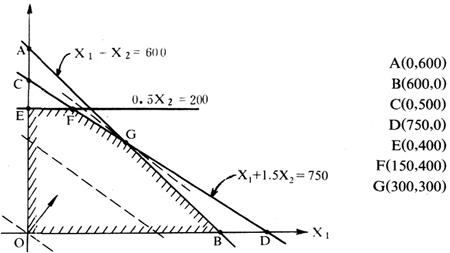
然后,画出约束条件直线,将约束不等式(1)变为等式x1+x2=600,在图中画出AB直线,进一步限制可行解区域在直线AB及其左下半平面。类似地根据约束不等式(2)和(3),分别画出CD和EF直线。
这样形成同时满足各约束条件的凸多边形区域OBGFE就是可行解区域。可行域有无穷多个点,是可行解的集合。可行域的各顶点O、B、G、F和E称为极点,根据极点的坐标上达成的可行解称为基底可行解。(2)从可行域中寻找最优解。已知Z=30X1+40X2,令Z取不同常数,可画出一族相互平行的直线,同一直线上的点有相同的Z值,直线按法线箭头所指方向推移,离原点愈远,Z值愈大。在这族直线中找到一条直线,它离原点最远且和可行域至少有一个极点相交(有时是和一条线段重叠),该交点坐标即为最优解。
它既满足约束方程组要求,又使目标函数达到最大值。本例最优解在交点G(x1=300,x2=300)取得,Z=21000。另外,也可以从原点开始,逐个极点迭代,取其Z值最大的点为最优解。
所以,线性规划问题的最优解如果存在,总是可以在其某个极点处求得。
上一篇:线性规划的解
下一篇:中国物资管理辞典目录