线性规划

出处：按学科分类—经济 经济科学出版社《西方经济学大辞典》第219页（1078字）

非负变量在线性约束下求线性目标函数最大(或最小)的问题。

在经济和生产管理中，许多问题可以近似地表示为线性规划问题(参见“影子价格”)。一个例子是，设某一经济可以分为两个部门，该两部门在一年中的经济活动可用以下投入产出表描述(见表)。

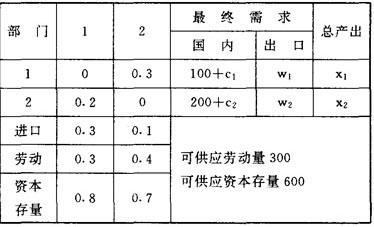
表中第一直列表示，生产第一部门1亿元产品，需要投入0．2亿元的第二部门的产品、0．3亿元的进口产品和0．3亿元的劳动，还要求有0．8亿元的资本存量，第二直列的意义类似。

最终需求分为国内消费和出口，其中的100和200分别为第一、二部门产品在国内的起码消费水平。

因为每一部门的总产出应等于投入量，故有

0．3x₂+100+c₁+w₁=x₁ (1)

0．2x₁+200+c₂+w₂=x₂ (2)

如果要求进口总额大于出口总额，则有

0．3x₁+0．1x₂＞w₁+w₂ (3)

再设劳动的最大供应量不超过300亿元，资本存量的最高限额为600亿元，则有

0．3x₁+0．4x₂≦300 (4)

0．8x₁+0．7x₂≦600 (5)

假设政府的目标是在(1)至(5)的约束下，选择非负的x₁，x₂，w₁，w₂和c₁，c₂，使得国内消费(高于起码水平)之和c₁+c₂达到最大。

令y₁=x₁，y₂=x₂，y₃=c₁，y₄=c₂，y₅=w₁，y₆=w₂，p=(0，0，1，1，0，0)，b=(－100，－200，0，300，600)

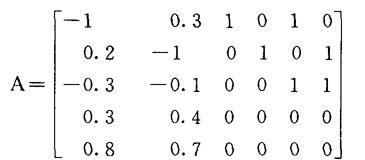
则问题可写成一个标准的线性规划：

maxp·y

s．t．Ay≤b

y≧0

现在已经有许多求解线性规划的方法，最典型的是单纯形法。