最优控制理论

出处：按学科分类—经济 经济科学出版社《西方经济学大辞典》第233页（1191字）

研究如何选择控制变量，从而求出一条使某目标值为最大(或最小)的轨道的理论。

考虑用导弹截击飞机的问题。导弹在时刻t的位置由坐标x(t)决定，现要求一"最优"轨道x(t)使某指标(例如导弹击中飞机的时间)达到最小或最大。而轨道x(t)又受控于某些变量u(t)(例如在时刻t的燃料消耗、冲刺方向与地平面的夹角等)。这里称x(t)为状态变量，u(t)为控制变量。

设u(t)可以在某一函数集合U中选择，问题将是从U中选择一个u(t)，从而决定x(t)，使该指标达到最大或最小。这类控制问题可表示为：

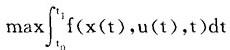
s．t．x′(t)=g(x(t)，u(t)，t)

x(t₀)=x₀，u(t)∈U

最优控制理论不仅在工程学上，而且在经济学上均有广泛应用。例如，设在时刻t资本存量为K(t)时产出为F(K(t))，而此产出有三种用途：消费C(t)，资本维修bK(t)及再投资K′(t)，即F(K)=C+bK+K′。设u(C)是消费为C时的效用，则最优控制问题

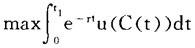
s．t．K′(t)=F(K(t))－C(t)－bK(t)

K(0)=K₀，K(t)≥0，C(t)≥0

就是从连续函数集合U中选择控制变量C(t)，从而定出状态变量K(t)使在[0，t₁]上的贴现总消费效用这个指标达到最大。

最优控制理论的研究由庞德里亚金(Pontryagin)等人在50年代开创。

他们证明：如果u(t)，x(t)是问题(1)的解，则一定存在非零函数λ(t)使得：

其中H(x(t)，u(t)，λ(t)，t)=f(x(t)，u(t)，t)+λ(t)g(x(t)，u(t)，t)称为哈密尔顿(Hamilton)函数；

(ii)H(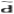(t)，(t)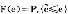，λ(t)，t)≥H(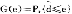(t)，u(t)，λ(t)，t)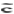，u∈U

即在任何时刻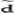(t)最大化H；

(iii)x(t₀)=x₀，λ(t₁)=0

由于(ii)表明H被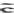(t)最大化，故以上必要条件又称为庞德里亚金最大值原理。