当前位置：首页 > 经典书库 > 公共经济学大辞典

米德增长模型

书籍：公共经济学大辞典

出处：按学科分类—经济经济科学出版社《公共经济学大辞典》第114页（7939字）

【内容介绍】：

剑桥大学教授詹姆斯·爱德华·米德(Meade，1961)构建了一种新古典经济增长模型，旨在表明最简单的古典经济体系形式能在均衡增长过程中运转的方式。

1．模型的基本假设

米德教授依据下列假设条件建立他的模型：

第一，存在一种自由放任的封闭型经济，这种经济是完全竞争的。

第二，规模收益率不变。

第三，在这种经济中生产两种商品——消费品和资本品。

第四，机器是经济中的惟一资本形式。

第五，所有机器假定都是一样的。

第六，消费品的货币价格固定不变。

第七，土地和劳动力得到充分利用。

第八，劳动力与机器的比率无论是在短期还是在长期都可能变化。

米德认为这一假定说明的是机器具有完全可变性。

第九，资本品与消费品之间具有完全的替代性。

第十，机器因老化而需要折旧，也就是说，机器在每一年都有一定比例的消耗，需要重置。

2．模型的基本框架

在上述这种想像的经济中，净产出的生产取决于下列四个要素：

第一，以机器形式表现的可利用的净资本存量。

第二，可利用的劳动力数量。

第三，土地和资源的可利用性。

第四，随着时间的推移，不断改进的技术知识状况。

上述这些关系可用生产函数的形式予以表达成：

Y=F(K，L，N，t)

式中各符号的经济含义是：

Y——净产出或净国民收入

K——现有的资本存量(机器)

L——劳动力

N——土地和自然资源

t——时间，意味着技术进步

假定土地或自然资源的数量是固定的，净产出在K、L和t增加的任何一年都可能增加。这种关系可以表示为：

△Y=V△K+W△L+△Y′

式中各符号的经济含义是：

△——在任何情况下都表示“增加”

V——边际资本产量或边际资本效率

W——边际劳动力产量或边际劳动力效率

Y′——用来取代t，表示因技术进步导致的收入增加。

边际资本产量和边际劳动力产量不同于资本－产出比率，因为它表明的是假定其他所有投入不变的情况下，资本增加一定量所导致的产出的提高。

在图1中，边际资本产量表明在劳动力数量L₁不变的情况下，资本从OK₁增至OK₂所导致的产出增加。在这种情况下，边际资本产量是AB／K₁K₂，这显然比资本－产出比率低，因为资本－产出比率是AC／K₁K₂。

图1 边际资本产量与资本－产出比率的关系

因此，“年度净产出率的提高(△Y)等于机器存量的增加(△K)乘以它的边际产量(V)，加上劳动力数量的增加(△L)乘以它的边际产量(W)，加上仅由技术进步引起的年度产出率的提高(△Y′)”。每年按比例的产出增长率是：

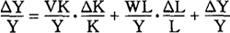
其中，

△Y／Y=按比例的产出增长率

△K／K=按比例的资本存量增长率

△L／L=按比例的劳动力增长率

△Y′／Y=一年内按比例的技术进步增长率

下面，用y、k、1、r来分别表示上述这些按比例的增长率，用U来表示比例性资本边际产量VK／Y，用Q来表示比例性劳动力边际产量WL／Y。

VK／Y表明的是作为利润支付给机器所有者的净国民收入的比例，而WL／Y表明的是作为工资而属于劳动力的国民收入的比例。现在，基本关系式成为：

y=Uk+Ql+r (1)

方程式(1)表明，产出增长率(y)是其他三项增长率加权总和，即用比例性边际资本产量(U)加权的资本存量增长率(k)，加上用比例性边际劳动力产量(Q)加权的人口增长率(l)，再加上技术进步增长率(r)之和。

但是，经济增长的实际指数是人均实际国民收入增长率，而不是国民收入增长率(y)。例如，如果总国民收入(y)每年提高10%，人口(l)提高8%，人均国民收入(y－l)每年将提高2%。人均实际国民收入增长率是：

y－l=Uk－(1－Q)l+r (2)

方程式(2)揭示出，人均实际国民收入增长率可以两种方法来提高：第一是通过用其比例性边际产量(U)加权的实际资本增长率(k)的提高，第二是通过技术进步增长率(r)的提高。

相反，人均实际国民收入增长率会受到以1减去比例性劳动力边际产量(1－Q)加权的人口增长率(1)的制约。

方程式(2)的这部分即［－(1－Q)1］表明了随着劳动力数量的增加(在土地和资本数量既定的情况下)收益递减的趋势。

有利于产出增长率的重要因素之一是经济中的年度资本积累率。

这个因素隐含在Uk一项中。U=VK／Y，k=△K／K，但是，△K(资本存量的增量)等于净国民收入中用于储蓄的部分。

因此，△K=SY，k=△K／K=SY／K。其中，SY代表每年通过储蓄而使资本存量增加的数额。

故此，Uk=VK／Y×SY／K=VS，且基本的增长关系式可以表达为：

y－l=VS－(1－Q)l+r (3)

米德教授在考察了决定实际人均国民收入增长率的主要因素之后，继续讨论了可能导致经济增长率在一定时期内变化的条件。假定l和r是既定的且不变，经济增长率的变化可能是由V、S和Q在一定时期内的行为决定的。

如果人口和技术进步没有变化，储蓄率的提高可能会提高人均资本而降低边际资本产量。可是，如果资本有可能替代土地和劳动力，那么，V的下降是很小的；如果有技术进步，V可能提高而不是下降。但是，土地和劳动力的数量在经济中假定是固定的，更多的人均资本就要被利用，与此同时，技术进步将会提高V。在这些条件下，人均国民收入增长率可能提高，继而可能导致S提高。

由于收入分配有利于增加上述因素引起的利润，S有进一步提高的趋势。可以认为，当人口不变(1=0)时，实际人均国民收入取决于资本积累率(VS)和技术进步(r)。

其方程式是：

y=VS+r (4)

如果除人口增长之外还假定技术进步率不变，人均国民收入增长率将会直接随着VS的变化而变化。

技术进步对国民产出(收入)的影响，可以用图2来说明。机器(资本)存量总额用横轴来表示，年度产出总量用纵轴来表示。OF₁是生产函数，表明的是机器数量和技术知识既定情况下的第一年生产的产出量。如果第一年的机器数量是OK，这一年的生产量将是KA。在点A的该曲线的斜率表明的是机器的边际生产率，随着沿该曲线向右移动，机器的边际生产率逐步下降。

这是因为像其他要素一样，收益递减法则也适用于机器。因此，在点C，机器的边际产量将低于在点AS的边际产量。在第二年，由于技术进步，新的生产函数成为OF₂。结果，虽然利用相同的机器OK，但生产却从KA增加至KB。同样地，利用OK₁数量的机器，生产从第一年的K₁C增加至第二年的K₁D。所以，技术进步导致年度总产出的增加。

图2 技术进步对国民总产出的影响

3．模型的分析

3．1 稳定增长状态

米德教授进一步考察了稳定经济增长状态。这是一种总产出(收入)增长率保持不变，因而人均国民收入增长率也保持不变的状态。

假定人口按不变的比率(1)持续增长，而技术进步率保持不变。

稳定经济增长状态要求存在下列三种条件，以保证总国民收入增长率不变：

第一，各种要素间的所有替代弹性都等于1。

第二，对所有要素来说，技术进步是中性的。

第三，利润、工资以及租金用于储蓄的比例都不变。

条件1和条件2意味着：利润(U)、工资(Q)以及租金(Z)在国民收入中各自所占的比例不变。因此，依据条件3，这些要素报酬中用于储蓄的部分占国民收入的比例保持不变。

令Sv、Sw和Sg分别代表来自利润(U)、工资(Q)和租金(Z)的储蓄，因而总储蓄就是：

由于按照条件1～3的规定，方程式(5)中的所有因素都是不变的。

可见，储蓄总额占国民收入总额的比例也是不变的。

国民收入增长率可以用如下基本关系式来表达：

y=UK+Ql+r (6)

其中，U、Q、l和r假定都是不变的。因此，由于y是不变的(因为这是稳定经济增长状态的要求)，故k也应当不变。我们知道，

k=SY／K (7)

但是，如上所述，S是不变的。因此，如果Y／K是不变的，则k也是不变的。

如果Y和K的增长率相同(这意味着y和k本身就是相等的，即y=k)，则Y／K是不变的。由此可得到如下明确的结论：如果资本存量增长率(k)等于国民收入增长率(y)，国民收入增长率将是不变的。

3．2 决定性增长率

均衡位置最终取决于资本存量的积累率。根据米德教授的观点，资本存量存在着一种决定性的增长率，它使得国民收入增长率等于资本存量增长率。

比这种“决定性或关键性增长率”(critical growth rate)或高或低的资本存量增长率不会使y和k相等。如果令a代表“决定性增长率”，那么，上述的基本关系式将成为：

a=Ua+Ql+r (8)

或者

这一基本关系式可以利用数字例子来证明。

令Q=1／2，1=2%，r=1%，U=1／4，则：

正是这个决定性增长率(在上述例子中是2)使得y=k，并在这种稳定增长水平上保持国民收入增长率不变。

不管在何时有任何偏离这种稳定增长水平的现象，各种力量就会介入，使资本存量增长率处于均衡水平。假定k或。在这种情况下，国民收入将以低于资本存量增长率的比率增长；结果，储蓄将下降，资本增长率会下降，从而使接近于决定性水平。相反，如果，则国民收入将以快于资本存量增长率的比率增长，储蓄和资本存量都会增长；结果，将提高到接近于决定性水平。