财政赤字对利率的影响：理论分析

出处：按学科分类—经济 经济科学出版社《公共经济学大辞典》第879页（20995字）

【内容介绍】：

长期以来，财政赤字对利率的影响问题一直是经济学家们的关注焦点，因为这一问题关系到财政赤字是否对民间投资具有抑制作用或产生排挤效应，以及是否对总需求具有刺激作用等根本性问题。

在这一问题上，理论界有两种对立的观点：一种观点认为，大量赤字对利率的影响很大，其理论依据是，信贷资金的供给和需求对利率的变化缺乏弹性，致使需求扩大或供给缩小到某一既定水平要求利率有大幅度的提高。另一种观点认为，赤字对利率的影响很小，原因在于财政上的债务与其他资本之间有高度的相互替代性，弥补巨额赤字的资金可在利率不变的情况下筹集到，故赤字再大也没有关系(凯甘，1988，第132页、第140页)。

针对这一争论已久的问题，我们根据现代利率决定理论模型，从不同的角度探讨财政赤字对利率的影响及其影响的实现机制。

1．封闭型经济中财政赤字对利率的影响

1．1 依据IS－LM模型分析赤字对利率的影响

我们首先应用传统的IS－LM模型来分析财政赤字对利率的影响(Siber，1970；Carlson and Spencer，1975)；Burrows，1979；Roley，1981)。

现假定：(1)财政赤字是由于增加财政支出引起的；(2)用发行公债的方式来弥补财政赤字。

根据宏观经济学的一般假定，下列等式存在：

C=C(Y_d) (1－1)

I=I(i) (1－2)

Y_d≡Y－T (1－3)

Y=C+I+G (1－4)

M_d／P=L(Y，i)

， (1－5)

M_s／P=L(Y，i) (1－6)

△G－△T=△M_s／P+△B／iP (1－7)

式中各符号的经济含义是：

C——实际私人消费

I——实际私人投资

i——市场利率

Y_d——实际可支配收入

Y——实际国民收入

T——实际税收收入(定额税)

G——实际财政支出

M_d——名义货币需求

M_s——名义货币供给

P——价格水平

B——无期限公债的供给量

偏微分系数表示函数变量间的关系。

(1－1)式表明，消费C为可支配收入的递增函数，可支配收入增加，消费也增加，但其绝对数量上的增加小于收入增加。(1－2)表明，投资是利率的递减函数，利率上升自然减少投资。

(1－4)式表示商品市场的均衡条件。

(1－5)式是流动性偏好函数。

式中的L表示货币需求量，L(Y，r)为货币余额的需求函数。表示交易量越大，所需现金余额用以完成交易的数量越大。

这种持有现金的动机通常属于交易动机。表示：(1)若持有现金而放弃证券，持有货币的人即牺牲利息收入，但享有持有现金的安全与便利；(2)利率越低，牺牲的利息收入越小，闲置现金余额越大，这种持有现金的动机称为资产动机。(1－6)式表示货币市场的均衡条件，亦即货币供给量的多寡取决于货币当局，在均衡的情况下，货币需求量等于其供给量。(1－7)式表示政府预算限制条件式。假定每张公债的定额利息为1个货币单位。

如果财政赤字全部由发行公债来融资，那么，(1－7)式可以写成：

△G－△T=△B／iP △M=0 (1－8)

充分就业情况下赤字对利率的影响 我们首先假定经济处于充分就业状态。在这种情况下，产出总量是社会当时所能生产的最大产量。故此，我们可以把产出或实际收入视为一定，亦即dY=0。

如图1所示，Y₀代表充分就业产出，最初的均衡点是E₀。

根据乘数理论，财政支出的增加可视为自发生性投资(autonomous investment)的增加，从而促使总需求扩张。如果财政支出的增加(赤字)是通过发行公债来融资的，那么，在商品市场上，一开始就会出现商品的超额需求，引起物价上升。换言之，由于财政支出增加，商品市场曲线从IS₀向右移至IS₁，Y₁－Y₀就是最初的商品超额需求。

图1 充分就业情况下赤字对利率的影响

另一方面，随着公债的不断发行，利率逐渐上升，导致民间投资降低。因而，商品的超额需求减少了Y₁－Y₀，但物价仍然继续上升。

由于物价上升会降低私人持有的货币的实际价值，民间部门为了使实际货币余额保持在起初的水平，就得卖掉手中的公债。这意味着实际货币需求增加，从而进一步促使利率上扬。

这种变化由货币市场曲线LM₀向左移动表示。

LM曲线和IS₁曲线的交点，只要在Y₀线(充分就业状态下的实际所得水平)右边的任一位置上，商品的超额需求就会存在，物价就将持续上升；与此同时，实际货币需求还在增加。

于是，LM₁曲线和IS₁曲线的交点变成了新的利率均衡点。结果，利率由i₀提高到i₃，其提高幅度等于这一时期内物价上涨率。

不充分就业情况下赤字对利率的影响 在经济处于不充分就业状态下，商品的生产或供给具有完全弹性，随时可以满足商品的需求，当然也就不存在商品的超额需求现象。

此时，我们可以假定价格水平是一定的。现在，假定财政支出增加所导致的财政赤字是由发行公债来融资的。

在这种情况下，财政支出增加的直接效果是使IS₀曲线向右上方移动，譬如移至IS₁。

此外，总需求增加引起产出增加，同时也增加了实际收入。故此，由于实际消费需求的增加，交易货币需求亦将增加。此时，如果货币供给量不变，货币的超额需求就会产生，市场利率随之上升。

债券需求增加，货币资产需求减少，货币总需求亦减。

市场利率一直上升到总需求与货币供给相等的点。

在这个过程中，货币流通速度加快，可维持商品交易总量的增加；而为财政赤字融资所发行的公债被货币资产需求的减少所抵消。

另一方面，由于市场利率的上升，减少了私人投资，当初增加的总需求量(Y′)减少了一部分。经过这样的变化，商品市场的供求均衡和货币市场的均衡同时实现，且利率亦上升。

这期间，因价格水平和名义货币供给量不变，所以，LM₀曲线依然保持在原来的位置上。新的均衡利率即为i₁。

图1明确地表示出，如果商品的总需求函数和货币需求函数是既定的，那么，在充分就业场合，财政赤字对利率的上升效应大于在其他场合财政赤字对利率的上升效应。其差异在于，前者会产生价格水平上升现象，且使实际货币供给减少，而最终只能使过度的实际超额货币需求相对扩大。

下面，我们将进一步分析虽然也是在不充分就业状态下，但在特殊的投资函数或货币需求函数的场合，财政赤字对利率的影响就会同上述情况大不相同。

第一，在货币需求对利率有弹性的情况下赤字对利率的影响。传统的凯恩斯经济学认为，在严重的经济萧条时期，有可能产生“流动性陷阱”(1iquidity trap)。所谓流动性陷阱，即人们越相信利率不会再下降，而它却越有可能达到最低水平的状态。

在这种情况下，对货币余额的需求增至无穷大，即L_r→∞。其原因在于，在低利率的情况下，人们害怕资本有损失，都想更多地持有货币以及流动性很高的资产，不愿持有长期债券，货币的需求成为完全弹性。

因此，虽然财政支出增加，有可能引起总需求增加及其引致的交易货币需求的增加，但是，由于人们手中持有大量的货币余额，财政支出的增加不会对利率有哄抬效应。

另一方面，如果私人部门难以全部吸收赤字公债，中央银行要设法消化一部分。

这样做的结果，与其说会导致货币供给增加，不如说会产生抑制利率的效果。

因为，按照凯恩斯的理论假说，流动性偏好的存在使利率降低到一定程度后，货币供给的任何增加都会被投机动机驱使的流动性偏好所吸收，从而使扩大货币供给的政策失去了降低利率的作用，反而有鼓励投资，增加就业的作用。

如果把上述讨论用IS－LM模型来分析，“流动性陷阱”因货币需求的利率弹性而可以认为趋于无穷大。所以，LM曲线将成为一条与横轴平行的直线。

即使财政支出增加，IS₀曲线向右移动，IS曲线和LM曲线相交所决定的均衡利率依然不变。

第二，在货币需求对利率无弹性的情况下赤字对利率的影响。

在货币需求对利率完全无弹性的极端情况下，LM曲线呈垂直状态，即图1中的LM₂。这时，即使经济处于不充分就业状态，实际总支出也受货币供给量的制约。

这样，实际收入则由以LM₂曲线所表示的货币市场来决定。财政支出增加(赤字)，纵然能使IS₀曲线向右移动，但是，随之而来的却是交易货币需求的增加，从而促使利率提高。

可是，货币资产的需求却不会因此而减少，因为，它对利率是完全无弹性的。在这种情况下，如果再发行公债为赤字融资，只能刺激利率进一步上升。这样，由于最初的实际产出受到货币供给余额的限制，市场利率不断上升，直至增加的实际总需求量减少为止。在这一过程中，货币需求量也要减少，并在既定的货币供给余额下达到均衡。结果，新的均衡利率在i₃形成。这虽然是在不充分就业的场合，但利率的上升程度却和充分就业场合的同样大。

这也是极端的货币学派的观点。

第三，在投资对利率无弹性的情况下赤字对利率的影响。所谓投资对利率无弹性，系指利率降至某一水平后，即使它再降低也无法使投资增加的情况。在投资对利率的变化呈现完全无弹性的场合，IS曲线呈垂直状态，即图1中的。

如果赤字支出把IS₀曲线平行向右移至IS₂，新的均衡利率则为i₂。可见，在这种场合下的利率上升，比投资对利率变化有弹性的场合要大。

综合上面三种特殊情况的分析，我们可以得出如下结论：在不充分就业情况下，货币需求的利率弹性和投资的利率弹性越小，财政赤字对利率上抬的压力越大。

资产效应和有价证券效应存在情况下赤字对利率的影响 有关消费支出的资产效应(asset effect)假说，虽然起源于皮古(Pigou)和哈伯乐(Herberler)的主张，但近年来作为商品生命周期学说的组成部分，由莫迪利亚尼(Modigliani，1971，p．9－84)承袭完善。

这种理论是，家庭现在的消费支出量，在家庭现有的纯资产及生存期间所能得到的全部所得的约束下，由整个生存期间的消费支出的最适分配来决定。因此，如果所有的资产量有净增加的话，短期的消费支出量也可以认为有某种程度的增加。在考虑资产效应的情况下，(1－1)式可作如下变更：

C=C(Y_d，a)

a≡M_s／P+△B／iP (1－9)

a表示私人实际净资产。这里，我们假定资产只包括货币和公债。

如果这种假设成立，依靠公债弥补赤字，其直接效应是把IS₀曲线移至IS₁；同时，由于私人持有的公债增加而使其净资产增加，继而资产效应又使其消费支出增加，导致IS₁曲线愈发向右移动，也许能达到IS₃。如果真是这样，新的均衡利率就是i₂，它比不存在资产效应的场合更高。

可见，如果实际支出的资产效应存在，财政赤字则具有哄抬利率的作用。

此外，我们还可以认为，私人净资产的增加，不仅影响消费行为，还影响个人的有价证券选择行为。

如果为了弥补财政赤字而大量发行公债，并且全部由个人购买，那么，在个人的净资产有所增加的同时，有价证券的构成就会发生变化。个人为了使其有价证券构成优化，过了一段时间也许想卖掉一部分公债，以增加货币持有量。

如果他真的这样做了，货币需求无疑要增加，我们称之为有价证券效应(portfolio effect)，亦称资产选择效应。如果把这种效应也考虑进来，上述的(1－5)式又可写成：

M_d／P=L(Y，i，a) (1－5′)

如前所述，赤字支出将使IS₀曲线移至IS₁；同时，利率由i₀上升到i₁。可是，发行公债却产生了有价证券效应，促使LM₀曲线向左移动。

倘若它移至LM₂，新的均衡点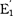点出现，i₂就是均衡利率。可见，有价证券效应对财政赤字哄抬利率起到了雪上加霜的作用。

综上所述，利用传统的IS－LM模型所做的分析，得到的结论是：几乎在所有的场合，财政赤字都有可能促使利率上升。

需要注意的是，我们上面所作的分析，主要集中于财政赤字是由财政支出的增加所导致的情形，但这不等于说由于减税导致的财政赤字，就不会对利率产生上扬压力。简单来说，减税可使消费者的实际可支配收入增加，从而增加实际消费支出。因此，IS₀曲线依然会向右移动，但通常是。所以，如果等量的赤字是由减税而不是由支出引起的，那么，减税引起的赤字所造成的IS₀曲线右移的幅度相对要小，最终所导致的利率上升幅度当然要小些。

1．2 依据三种资产模型分析赤字对利率的影响

这里所谓的资产，除了货币和公债外，还包括私人长期债券，即公司债券。这三种资产模型是由费里德曼(Friedman，1978)和罗利(Roley，1983)提出的。

为了简便起见，模型中的均衡条件式全部以线性形式表示。另外，我们假定资产效应和有价证券效应都存在。

Y=c₁Y+c₂i_E+c₄A+c₅G－c₁T

c₁＞0，c₂＜0，0＜c₄＜1，c₅＞0 (1－10)

M=m₁Y+m₂i_E+m₃i_B+m₄A

m₁＞0，m₂＜0，m₃＜0，

0＜m₄＜1 (1－11)

E=e₁Y+e₂i_E+e₃i_B+e₄A

e₂＞0，e₃＜0，0＜e₄＜1 (1－12)

B=b₁Y+b₂i_E+b₃i_B+b₄A

b₁＜0，b₃＞0，0＜b₄＜1 (1－13)

A≡M+B+E (1－14)

式中各符号的经济含义如下：

Y——国民收入

G——财政支出

T——税收收入

A——资产余额

M——货币供给量

B——公债供给量

E——公司债券供给量

i_E——公司债券利率

i_B——公债利率

c_j，m_j，e_j，b_j(j=1，…，5)表示的是各函数关系的系数。这些系数的符号可作如下假设：对上述三种资产需求的利率弹性都为正，对其他资产的利率弹性为负，对总资产的利率弹性为正。

在这个模型中，假定经济处于充分就业状态，而且价格水平不变，即P=1。这样，每个变量的名义值和实际值相同。

(1－10)式表示的是商品市场，(1－11)式表示的是货币市场，(1－12)则为公司债券市场，(1－13)表示的是公债市场，(1－14)式是资产的定义。如(1－10)式中的c₂i_E所示，企业主要依靠发行公司债券来筹集投资资金。此外还假定，投资主要受公司债券利率的影响；资产的选择受各种资产收益率的影响：货币的收益率为零。

货币供给以及公债供给都是由政府部门所掌握的政策变量，故视其为外生变量。企业完全依赖公司债来维持实际资产的积累，并假定公司债供给余额等于资本存量价值。在一定期间内，如果物质资本存量不变，则公司债余额也可视为一定。由(1－11)式～(1－14)式得知，三种资产的需求受总资产余额的制约。

如果以总资产余额作为解决问题的前提，且能决定其中任何两种资产的需求，那么，另一种资产的需求也就同时确定下来。

也就是说，在三种资产市场均衡条件式中，无论哪一个公式都不是独立的。为此，在这些条件式中，必须消去一个。

我们暂且先放弃公司债的均衡条件式。

在新的方程组中，内生变量是i_E、i_B和Y。

要想利用此方程式来搞清赤字对利率(公司债利率)的影响，首先得描绘出具有i_E和Y坐标轴的商品市场均衡(IS)和货币市场均衡(LM)图示，即图2。图2中引人注目之点就是，促使LM曲线移动的参数中，包括公债利率i_B。

根据(1－11)式，。

亦即如果公债利率上升，LM曲线就往右移动。

图2 财政赤字对利率的影响：三种资产模型

依赖发行公债融资的赤字支出增加，将促使IS₀曲线往右移动；私人持有公债的增加所带来的资产效应，将继续发挥作用。因此，IS曲线就会更往右移动，最终达到IS₁。

在这一变化过程中，总需求增加，交易货币需求亦增加，公司债利率便上扬至i_E1的位置上。

另一方面，如果因私人持有公债的增加带来的有价证券效应，促使LM₀曲线向左移动，这将进一步上推利率水平。

但是，如果在大量发行公债的同时，提高公债利率，如上所述，LM曲线将向右移动，利率将有下降的趋势。在新的均衡中，公债利率是否比当初的水平提高了，这要视LM₀曲线向相反方向移动的相对大小来定。

在以公债为赤字支出融资的场合，根据政府预算限制式，dG=dB成立。以此式为前提，为了弄清财政赤字在资产市场中对公司债利率和公债利率有何影响，需要把收入Y假设是既定的，并根据(1－11)式和(1－13)式，求出每个有关利率的偏导系数：

=［－m₄b₂－m₂(1－b₄)］／［m3b2－m₂b₃］＞0 (1－15)

=［m₃(1－b₄)+m₄b₃］／［m₃b₂－m₂b₃］ (1－16)

根据布瑞纳德－托宾(Brainard and Tobin，1968，p．99－122)的有价证券余额条件，假定系数之间存在着如下函数关系：

m₁+e₁+b₁=0

m₂+e₂+b₂=0 (1－17)

m₃+e₃+b₃=0

m₄+e₄+b₄=1

(1－15)式表明，以公债融资的赤字支出将使公债利率上升。

另一方面，在(1－16)式中，分母之值是正的，分子之值是正是负尚不能确定。但作为发行公债的结果，(1－16)式还是给出了LM₀曲线是向左还是向右移动的条件。

现在，如果财政赤字导致新的均衡，我们不一定限于在此均衡中求得与LM曲线原位置一致的条件。根据(1－16)式，如果=0，则m₃(1－b₄)=－m₄b₃；根据(1－17)式，如果b₃=－(m₃+e₃)，即可得出m₃／e₃=m₄／(1－b₄－m₄)。

当这个条件式成立时，资产市场的新均衡就会和原来的均衡状态一样。

现在，令

θ≡m₃／e₃ (1－18)

θ^*≡m₄／(1－b₄－m₄)

三m₄／e₄ (1－19)

从(1－11)式和(1－12)式中可以看出，m₃表示公债与货币之间的替代程度，e₃代表公债与公司债之间的替代程度。θ无疑就是公债替代货币的程度与公债代公司债的程度之比率。m₃和e₃两者之值都是负的，因而θ＞0；m₄和(1－b₄－rn₄)两者之值都是正的，因而θ^*＞0。

如果公债对货币的替代效应大于公债对公司债的替代效应，即m₃＞e₃，则θ大；相反，如果公债对公司债的替代效应大，而对货币的替代效应小，即e₃＞m₃，则θ小。如果公债与公司债是完全替代的(e₃=∞)，则θ=0；如果公债与货币是完全替代的(m₃=∞)，则θ=∞。因此，原则上，0≤θ≤∞。可是，根据(1－17)式、(1－18)式和(1－19)式，如果θ≥θ^*和θ＜θ^*，则，0。

我们可以用图2来说明这种关系。

如果θ=θ^*，由于有价证券效应的两种相反作用力的抵消，结果LM₀曲线即不向左也不向右移动，因此，公司债利率只有在交易货币需求增加时才可能上升，新的均衡水平变成i_E1。

如果θ＜θ^*，即公债对公司债的替代效应非常大，而公债对货币的替代效应又非常小，那么，LM₀曲线将往左移动。

这两种替代效应之间的差距越大，公司债利率的上扬程度也越大。

如果达到LM₁，新的均衡公司债利率就成为i_E2。

如果θ＞θ^*，即公债对货币的替代效应相当大，而它对公司债的替代效应却很小，LM₀曲线将往右移动。

公司债利率也许会下降到i_E1以下。并且，如果θ比θ^*大很多，新的均衡公司债利率也许会与原来的水平i_E0一致或比它低。

综上所述，我们得出如下结论：第一，依据三种资产模型所作的分析，用公债融资的财政赤字有哄抬公债利率之效，但公司债利率未必同样上升，有时反而可能下降。

第二，一般来说，短期公债对货币的替代效应，比对公司债的替代效应要大；而长期公债对公司债的替代效应，要比对货币的替代效应大。从这个意义上说，用公债给赤字融资时，发行短期公债比发行长期公债要好些，因为，前者融资的赤字对利率的上扬压力相对小一些。

2．开放型经济中财政赤字对利率的影响

即使财政赤字引起短期利率上升，但如果其结果导致外国资本大量流入，当初的利率上升有可能被抑制。

同时，如果利率上升引起对外资本收支变化，商品和劳务进出口变化引起经常收支变化，那么，汇率的变化将引起利率的变化。因此，要想深刻了解财政赤字对利率的影响，还需要根据包括资产、商品和劳务的对外贸易模型来分析。

2．1 依据有价证券平衡理论分析赤字对利率的影响

在本国证券与外国证券为不完全替代的情况下，利率的决定条件可作如下假定(Frankel，1979，p．610－613；Hutchison and Throop，1985，p．28－31)：

lnq^e－lnq=n(r－r^*)－nψ^e (2－1)

式中各符号的经济含义如下：

q——实际汇率

q^e——预期实际汇率

r——本国证券的实际利率

n——时期(跨越年度)

ψ^e——预期均衡利率差额或风险报酬(取决于国内外证券不能替代的程度)

如果财政赤字导致本国的利率上升，从而产生本国利率高于国外利率的情形，那么，国外资本流入将增加，汇率就会提高。当汇率上升到某一水平时，外国投资者看到由于对外投资的增加，有价证券的不均衡危险可能比对外投资的收益率还要大，他们就要减少对外投资。

所以，本国利率将会逐渐下降，汇率与利率又回到原来的水平。但是，在这一恢复过程中，外国的利率假定是既定的。

倘若财政赤字是暂时的，如上所述，本国利率的提高与汇率的上升也都是暂时的。如果财政赤字长期存在，预期公债大量累积，那么，风险酬金逐渐增加；又由于外国资本流入增加，本国利率高于外国的利率差额减少，所以，汇率逐渐趋于下降。

但是，在本国利率比原来的水平还高的情况下，财政赤字对私人支出可能产生部分排挤效应。

这可以说是短期效果。

2．2 依据支出理论分析赤字对利率的影响

支出理论模型假定本国产品与外国产品不是完全替代的(Hutchison and Throop，1985，p．31－33)。在这些产品的需求与供给变化的同时，某些均衡相对价格也会相应发生变化。

于是，我们对本国产品和外国产品的均衡条件分别作如下假定：

Y=A(r)+G+NX(q)

， (2－2)

Y^*=A^*(r^*)+NX^*(q)

， (2－3)

式中各符号的经济含义如下：

Y——实际国民生产总值

A——本国私人实际支出

NX——对外经常账户净收入

r——实际利率

q——实际汇率

*——外国的情况(假定外国只有一个国家)

(2－2)式是本国商品和劳务市场的均衡条件，(2－3)式是外国的商品和劳务市场的均衡条件。我们首先假定，本国和外国都存在着长期均衡的充分就业状态，故视Y为一定。又假定本国证券与外国证券是完全替代的，证券买卖在国内外都是自由的。因此，由于国内外的套利交易，下面的均衡条件式成立，但为了简化，假定不存在风险酬金：

r=r^* (2－4)

在(2－2)式、(2－3)式以及(2－4)式所形成的方程组中，内生变量是r、r^*和q。

现在，我们以图示说明满足(2－2)式均衡条件的r与q之间的关系，满足(2－3)式均衡条件的r^*与q之间的关系，并分别以图3中的G₀线和G₀^*线来表示。

图3 财政赤字对利率的影响：支出理论

现假定均衡点为E₀。

此时，由于增加本国的财政支出而产生的赤字，导致本国商品和劳务的需求增加，最终促使G₀线往左上方移动。可是，在实际汇率一定的情况下，国内吸收能力的增加受到限制，要想恢复均衡，必须提高实际汇率。此外，如果财政支出的增加，引起对国外商品和劳务的需求，那么，涉外部门的商品和劳务的出口以及对外经常净收入将增加。不管程度大小，它们都将促使G₀^*线向左上方移动。

在这种情况下，假定外国商品的需求增加小于本国商品的需求增加，比如说，新的均衡点为E1。在这个新的均衡点上，两国的利率水平通过国内外的套利交易后相同，但实际汇率比原来的水平高，即由q₀上升到q₁。

实际汇率的上升程度，取决于外国商品价格变动引起本国商品价格水平上升的相对大小。可见，本国发生财政赤字，将使本国及外国的实际汇率一并上升，但其差额未变。

2．3 依据开放型经济的LS－LM模型分析赤字对利率的影响

在开放性经济中，IS－LM分析模型可作如下假定(Dornbusch and Fischer，1984，p．615－692)：

Y=A(i，y)+G+NX(y，y^*，q) (2－5)

，，，，

M／P=L(i，y) (2－6)

，

BB=NX(y，y^*，q)+CC(i－i^*－ε) (2－7)

式中的各符号的经济含义如下：

M——名义货币供给

P——本国价格水平

i——本国名义利率

BB——本国国际收支

CC——本国资本收支(对外资本净收入)

q——实际汇率

其中，实际汇率可以表示为本国货币的直接汇率(e)乘以外国价格水平(P^*)，再除以本国价格水平(P)，即

q=eP^*／P

如果把ε作为汇率的预期变化率，那么，

ε=(e′－e)／e

式中，e′是本国货币的直接汇率的现时预期。

其他符号与(2－2)式和(2－3)式中的符号含义相同。

(2－5)式代表商品和劳务市场的均衡条件。实际汇率的贬值(q的上升)相对地驱使外国商品和劳务的价格上升，增加本国的净出口NX。但此刻，假定本国及外国的进口需求的实际汇率弹性充分大。(2－6)式代表本国货币市场的均衡条件，(2－7)式是国际收支的函数关系式。在该式中，对外资本净流入(CC)是本国利率与外国利率之差的增函数。

但是，我们假定，不论本国还是外国都只存在一种证券，本国证券与外国证券是完全替代的，并把各国证券的年息分别视为本国利率及外国利率；同时，假定国内外的资本流动是完全的。此外，如果外国证券的所有者在证券到期时，只要把外国证券的本利总额加上汇率的上升率即可。换言之，在这种情况下，由于本国利率高出外国利率的部分只是汇率的上升率，结果，对外资本净流入被视为用预期汇率来调整的对外利率差额的增函数。

在(2－5)式～(2－7)式所形成的方程组里，外国的实际国民生产总值(Y^*)、外国的利率(i^*)、外国的价格水平(P^*)以及汇率的预期变化率(e)是外生变量。本国经济假定处于不充分就业状态，则本国的价格水平(P)视为不变。

本方程组中的内生变量是i、Y和q。

根据(2－5)式，在q一定的情况下，i与Y之间的关系可用图4中的IS₀曲线来表示。

这里，q是参数。比如说，如果直接汇率(e)上升，在两国的相对价格水平不变的情况下，q就会上升。而后，对外净出口增加，IS曲线将往右移动。(2－6)式表达了国内价格水平一定时的i与Y之间的关系，并用LM₀曲线来表示。BB₀曲线代表国际收支均衡。在这里，假定国内外的资本流动对对外利率差额的反应极其灵敏，而且这种资本流动使经常收支的不平衡得到充分抵消。因此，国际收支平衡只有在两国的利率接近相同时(或更确切地说，只有i=i^*+ε)才存在。BB线以上部分是指国际收支为黑字，BB线以下部分是指国际收支是赤字。

由于已知i=i^*+ε₀，所以，(2－6)式就可以Y来决定。同时，正因为这个条件存在，汇率e可以调整成实际汇率q，并在IS线和BB线的交点E₀处得到决定。

可见，这个模型表明，开放性经济中的金融市场的调整比商品和劳务市场的调整，速度更快更有效。

让我们根据这个模型来分析财政赤字对利率的影响。现在的均衡点是E₀。由于政府财政支出增加或税收收入减少导致的赤字，用发行公债来融资。

财政支出增加将直接增加总支出，税收收入减少先通过增加消费支出，而后带动总支出的增加。所以，在初始利率和汇率水平的场合，商品和劳务将产生超额需求，IS₀曲线往右移动。

它引起商品和劳务实际产出增加，实际所得也随之增加。

与此同时，交易货币需求增加，推动本国利率上扬。当本国利率水平比外国利率水平相对高(称之为对外利率差额)时，外国资本的流入就会增加。当外国资本流入源源不断时，汇率就会上升。

汇率上升意味着进口价格下降，本国商品价格相对提高。所以，需求将从本国商品转向外国商品，对外净出口将会减少。这意味着IS₁曲线往左移动。在此移动过程中，本国利率可能要下降。

只要本国利率高于外国利率水平，外国资本的流入就会持续下去，汇率就会不断上升，而对外净出口也不断减少，最终IS₁曲线又回到IS₀线的位置上，即本国利率等于外国利率，汇率停止上升，新的均衡出现。但需要注意的是，新均衡场合比原均衡场合的汇率要高，商品和劳务出口水平将下降，尽管利率水平仍和原来的一样。

由此可见，在开放性经济中，财政赤字引起本国利率水平暂时上升，由此带来的外国资本的流入，使得本国的民间支出未受影响，也没有排挤效应发生；但由于引起汇率上升，从而对本国商品的外国需求产生了排挤效应。

上述分析包含一个假设，即汇率的预期变化率不变。

但是，如果投资者根据汇率的预期变化采取投机行动，结果会是怎样?

假定财政赤字是暂时的，并且投资者把它所引起的本国利率的上扬看成是暂时的，把预期汇率的上升也断定是暂时的，相信不久的将来汇率还会回到原来的水平上。于是，汇率的预期变化率ε会上升。在某一时点的特定对外利率差额的情况下，这种预期的变化，使得投资者对外国证券的需求超过对本国证券的需求。因此，在新的均衡点上，汇率的上升比ε不变的场合要小，但新的均衡利率比原来的均衡利率水平要高。

于是，i₂=i^*+ε成立，由于ε₁＞ε₀，则i₂＞i₀。

图4 财政赤字对利率的影响：开放型经济的IS－LM模型

3．财政赤字对名义利率和实际利率的影响

为了弥补巨额财政赤字，政府单靠发行公债，可能会导致市场利率水平明显上升。

为了抑制利率上扬，政府采取的措施之一是由中央银行购买市场上的公债，就是所谓的财政赤字货币化(monetization)。财政赤字货币化是一种过渡性措施，它在短期内具有抑制市场利率的效果，在中长期有可能引起通货膨胀，也会使市场利率上涨。

在通货膨胀的情况下，财政赤字不仅影响名义利率水平，也影响实际利率水平。

名义利率与实际利率的差异在于通货膨胀因素。

我们利用静态模型来考察财政赤字对名义利率和实际利率的影响。该模型体系可作如下假定(Bailey，1971，74－76)：

C=C(Y_d) (3－1)

I=I(i－π^e) (3－2)

Y_d≡Y－T (3－3)

Y=C+I+G (3－4)

M／P=L(Y，r+π^e) (3－5)

，

i=r+π^e (3－6)

π^e=π≡(P－P_－1)／P_－1 (3－7)

G－T=△M／P+△B／iP (3－8)

式中的各符号的经济含义如下：

r——投资的实际边际收益率

π——现实通货膨胀率

π^e——预期通货膨胀率

(3－2)式表明，实际投资需求是实际利率的减函数，而(3－5)式表明，货币需求是名义利率或投资的实际边际收益率加上预期通货膨胀率的减函数。

这是因为，持有货币而不是债券，牺牲了债券的市场利息。

如果存在通货膨胀，无论是货币还是债券，其实际价值都有所损失。如果持有货币而不是实物资本，付出的不仅是这种实物资本的实际收益，还有通货膨胀所带来的货币实际价值的损失。(3－6)式是资产选择的均衡条件式。

［预期通货膨胀的发生，把债券和货币的本利的实际值按预期通货膨胀率贬值，实际利率为i－π^e－iπ^e。要在债券、货币、实物资本三者之间做出无差别的选择，只有在它们各自的实际收益率都相同的时候。

因此资产选择的均衡条件为r=i－π^e－iπ^e。如果iπ^e相对很小，可忽略不计，则r=i－π^e，由此，得到r=i+π^e］预期通货膨胀表示为现实通货膨胀的线性函数，即(3－7)式。(3－8)式是政府预算限制式，但为简化，公债的利息支付忽略不计。

在图5中，IS₀线就是(3－4)式所表明的商品市场的均衡条件，LM₀就是(3－5)式所表明的货币市场的均衡条件。价格水平是P₀。这两条曲线的交点决定了均衡利率。

同时，由于预期通货膨胀率是零，故名义利率等于实际利率。

假定E₀是不充分就业的均衡点。政府用发行公债弥补由于财政支出增加导致的赤字。总需求增加引起产出增加，价格水平未变。

由于实际产出(所得)增加，引起交易货币需求增加，使得市场(名义)利率和实际利率都上升。表现在图5上，如果IS₀线移至IS₁线，则i₀就上升至i₁或r₁。

假定E₁是自然失业率水平或长期均衡产出水平的均衡点。中央银行为了控制住市场利率，在市场上收购了大量的公债。

由于财政赤字的货币化，民间部门持有的货币量增加，利率会下跌。

表现在图5中，LM₀曲线向LM₁曲线移动，利率由i₁下降至i′。利率下跌将刺激投资，故短期内可能提高实际所得和价格水平。随着实际所得的增加，实际货币需求也增加，利率转而上扬(i′→i₀)，有人称之为“快速恢复效应”(Mayer，1976)。

图5 财政赤字对名义利率和实际利率的影响

在E₂点，利率水平虽然比实行财政赤字货币化时的水平(即i₁)为低，但由于其间产生的价格水平的上涨导致实际货币余额下降了，货币的实际超额需求旋即发生，利率水平上升得更甚。利率上升将导致投资需求下降，产出亦随之减少。

这可用LM₁曲线向左上方移动来表示。只要商品市场存在超额需求，价格水平就有上涨的可能，实际货币余额就有下降的趋势。

所以，在自然失业率水平(Y₁)的场合，LM₁曲线向左上方移动，直至同IS₁曲线相交为止。这样，新的均衡利率同赤字货币化时形成的均衡利率处于相同的水平。

但是，新的均衡与原来的均衡有差异。在新的均衡下，名义货币余额居高不下，价格水平亦如此。

同时，这种现实通货膨胀将引起预期通货膨胀；而在新的长期均衡中，预期通货膨胀可以完全调整为现实通货膨胀。因此，商品市场与货币市场在E₁点同时达到均衡，资产选择的均衡亦存在。

这样，名义利率大致等于投资的实际收益率或实际利率加上预期通货膨胀率，即r₁+π^e=i₂。在此场合，由于货币市场依赖于名义利率，所以，货币市场均衡曲线可以说是LM₂曲线。

(可是，图中的LM₂曲线与IS曲线的交点没有任何意义。因为在这种情况下，名义利率与实际利率相离，LM₂曲线的纵轴表示的是名义利率，这与IS曲线表明的实际利率不同)

总之，在自然失业水平的情况下，财政赤字的货币化，在短期内虽然降低利率，但在长期内将引起通货膨胀，导致名义利率上升。

从长期来看，实际利率却依然如初。在不充分就业或衰退的情况下，财政赤字货币化，价格水平不会有太大的上升，预期通货膨胀不一定会产生，而由预期通货膨胀所引起的利率上升是否会出现尚属未定。

4．结语

我们根据不同的模型从不同的角度，在理论上探讨了财政赤字对利率的影响。就我们使用的模型所进行的分析来看，财政赤字对市场利率有上抬的压力。

但需要指出的是，我们所用的模型都比较简单，而且都是静态均衡模型，而赤字与利率的关系远非如此简单，故以这些模型所进行的利率分析，在一定程度上存在着局限性。

此外，我们还应该注意到，有关财政赤字对利率的影响，理论界一直争论不休。在理论上，美国罗切斯特大学巴罗教授(Barro，1974)在阐述李嘉图对等理论时曾指出，财政赤字对利率没有影响。进入80年代以来，许多学者对财政赤字与利率之间的关系作了大量实证分析，结论是赤字与利率之间没有必然联系。

。【参考文献】：

财政赤字对利率的影响：经验分析(Effects of Fiscal Deficit on Interest Rates：Empirical Analysis)

利率决定论(Theory of Interet Rates Determination)

Bailey, M. G. , 1971, National Income and Price Level, Second cd. .

Barro, R. J., 1974, Are Government Bonds Net Wealth, Journal of Political Economy.

Brainard, W. C. and J. Tobin, 1968, Pitfalls in Financial Model-Building, American Economic Review.

Burrows, P., 1979, The Government Budget Constraint and the Monetarist-Keynesian Debate in S. T. Cook and P. M. Jackson ed. Current Issues in Fiscal Policy.

Carlson, K. M. and R. W. Spencer, 1975, Crowding Out and Its Critics, Federal Reserve Bank of St. Louis Review.

Dombusch, R. and S. Fischer, 1984, Macroeconomics, Third edition.

Frankel,J.A.,1979, On the Mark: A Theory of Floating Exchange Rates Based on Real Interest Differentials, American Economic Review.

Friedman, B., 1978, Crowding Out or Crowding In? Economic Consequences of Financing Government Deficits, Brookings Papers on Economic Activity.

Hutchison,M.M.and A.W.Throop,1985,U.S. Budget Deficits and the Real Value of the Dollar, Federal Reserve Bank of San Francisco Economic Review.

Mayer, T.,1976,The Interest Rate Snap-Back and Its Implication for the Keynesian-Quantity Theory Dispute, Banca Nezionale del Lavaro Quarterly Review.

Modigliani,F.,1971,Monetary Policy and Consumption,in Consumer Spending and Monetary Policy: The Linkages,Federal Reserve Bank of Boston.

Roley,V.,1981, The Financing of Federal Deficits: An Analysis of Crowding Out, Federal Reserve Bank of Kansas City, Economic Review.

Roley,V.,1983, Asset Substitutabity and the Impact of Federal Deficits in L.H.Meyer ed. , The Economic Consequences of Government Deficits.

Siber,W.L.,1970,Fiscal Policy in IS - LM Analysis: A Correction, Journal of Money, Credit and Banking.

凯甘，P．主编，1988，《赤字经济》，中国经济出版社中译版