复数

出处：按学科分类—自然科学总论 天津人民出版社《自然辩证法辞典》第604页（564字）

形如a+bi的数。

其中a与b是实数，记为a=Re(a+bi)，b=Im(a+bi)，i为虚数单位(i²=－1)。复数也可表为平面直角座标系中的点(a，b)或极座标系中点(r，g)。其中r=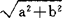，g=arctan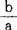。表示复数的平面称为“复数平面”。

复数的产生与发展经历了漫长的历史时期。虽然数学家们早在16世纪中叶已经遇到了复数，但是却一直不肯承认它是数。例如，卡尔丹诺(Cardano)在1545年将40表示成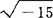(5+)(5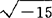－)，但他总感觉像是受到了良心的责备，并称这种数为“神妙”的。之后，他在解三次方程时又遇到了这种数。

当时由于人们看不到复数的实际应用，所以许多数学家仍认为这种数“无用”且“玄”。经过一个多世纪的怀疑后，17、18世纪生产与数学的需要，终于迫使数学家们必须引进复数，直到18世纪末、19世纪初，人们找到了复数的几何解释及物理意义后，复数才在物理等一些实际部门得到初步的应用。

数发展到复数系并没有完结，数学家们正在探讨是否可以建立包含复数系在内的新的超复数。四元数就是其中的代表。

一般说来，复数无序，不能比较大小。复数对于开平方运算是封闭的。

复数产生的最初总是以实数相对立的形式出现，但最后终于在复数系中统一起来，复数a+bi的表达形式，就是一个完美的对立统一关系。