集合论悖论

出处：按学科分类—自然科学总论 天津人民出版社《自然辩证法辞典》第838页（750字）

按照性质的不同，集合论悖论可分为两类，逻辑——数学悖论和语义学悖论。

逻辑——数学悖论是指仅借助于逻辑和数学的符号而得以构造的悖论。从数学的历史发展来看，这类悖论主要是指布拉里——福蒂(Burali——Forti)悖论、康托悖论和罗素悖论。语义学悖论是指“对于这种悖论的构造来说，象‘表明’、‘描述’、‘真’等这样一些语义项是必不可少的”，此外，在这类悖论的构造中还必须进行语义的分析。语义学悖论主要是指撒谎者悖论、理查德(Richard)悖论和格里林(Grelling)悖论等。在已知的集合论悖论中，罗素于1902年提出的悖论是影响最大的。这一悖论可表述为：由于对于任一集合都可以考虑其是否属于自身的问题，因此，依据概括原则，就可以从谓词“不属于自身”出发去构造出一个新的集合S。

它是由所有那些不属于自身的集合所组成的，即S₀={x|x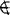x}由于S₀也是集合，因此，又可以进而考虑“S₀是否属于自身”的问题。根据排中律，只有两种可能，即要么S₀∈S₀，要么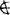S₀S₀。

但是，如果S₀∈S₀。则由S₀的定义可得出S₀不属于自身，即S₀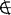S₀，这是自相矛盾的。而如果S₀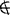S₀。则由于S₀不属于自身，所以，由S₀的定义可知S₀属于S₀，即S₀∈5₀，这也是自相矛盾的。

因此，矛盾是不可避免的。这就是有名的罗素悖论。

由于在这个悖论中所使用的论证方法是很简单的，并且在数学中又是常用的，所以，这个悖论使整个数学界大为震惊。为了从集合论中排除这个悖论，罗素提出了分支类型论。

但是，根据这个理论，甚至想发展通常的实数理论出变得很困难。另一方面，这个悖论以及布拉里——福蒂(Burali——Forti)悖论都表明，对于集合的定义方法应当加以限制，从而导致公理集合论的产生。