模糊数学

出处：按学科分类—自然科学总论 天津人民出版社《自然辩证法辞典》第911页（1366字）

研究和处理模糊事物和现象的数量关系的新兴数学分支学科。

1965年，美国自动控制专家、加利福尼亚大学L．A．查德教授发表题为《模糊集合》(Fuzzy Sets)的论文，首次把数学应用到模糊现象领域，由此开拓出数学的一个新领域。

模糊数学是建立在模糊集合论基础上的数学。模糊集合是相对明晰集合而言的另一类集合。

明晰集合的基本特征是，一个对象对于给定的集合，要么属于，要么不属于，二者必居其。

如果我们用“1”表示“属于”关系，用“0”表示“不属于”关系，则明晰集合的这一特征可用特征函数A(u)来表示：

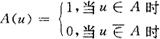
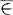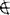其中u表示对象，A表示集合，∈表示属于，(或)表示不属于。模糊集合的基本特征是，不存在非此即彼、截然分明的界限，一个对象对于它，并非具有简单的“属于”或“不属于”关系，只是有隶属程度上的差异。

模糊集合的这一特征可用隶属函数来刻划。隶属函数是将特征函数由二值{0，1}推广到[0，1]闭区间上的任意值，也就是用0－1间的一个实数去描述所讨论的对象U具有某种性质的程度，这个数叫作“隶属度”。

隶属函数通常用μ(u)来表示，其中0≤μ(u)≤1。隶属函数在模糊数学中占有重要地位，是用数学方法描述模糊性的关键。它的确定，是一个比较复杂的问题，在很多情况下是根据经验或统计来决定的。模糊数学的创始者L·A·查德曾给出“年轻”和“年老”这两个模糊子集的隶属函数。

以年龄为论域U，取U=[0，100]，U上的模糊子集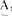=“年轻”，A₂=“年老”，可分别用隶属函数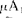(u)和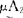(u)来表示：

模糊子集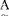的隶属函数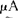(u)与明晰集合A的特征函数A(u)既有区别，又相互联系，有着辩证统一的关系。当隶属函数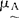(u)的值域只取[0，1]闭区间的两个端点0和1两个特定值时，便退化为特征函数，模糊子集也就退化为明晰集合。

这表明，明晰集合是模糊集合的特殊情况，模糊子集是明晰集合的自然延伸和推广。

在模糊数学理论研究中，分解定理和扩张原则的作用是十分重要的。

分解定理说的是，任何模糊集合的问题都可以通过某种特定的方法化为明晰集合的问题来加以处理。扩张原则说的则是，可以把明晰数学的方法扩展到模糊数学里去。

分解定理和扩张原则的提出，沟通了模糊数学和明晰数学两大数学领域，使它们在思想方法上发生了密切联系，成为整个数学机体中不可分割的两个方面。

模糊数学自1965年诞生以来，不论在基础理论研究还是在应用研究上都已取得显着的成果。

首先，模糊数学的思想方法已广泛渗透到数学的各个领域，传统数学的许多理论、分支学科已经被“模糊化”，如模糊向量、模糊矩阵、模糊映射、模糊变换、模糊图论、模糊概率、模糊统计等。其次，模糊数学的应用已广泛涉及到科学技术的各个部门，如物理学、化学、生物学、医学、心理学、地质学、气象学、逻辑学、语言学、经济学、情报学、管理学、系统科学、电子学以及人工智能等。同时，它在设备控制、机器检修、石油、采矿、冶金、地质、建筑、农业、林业等国民经济领域已得到初步的应用。