临界点理论
出处:按学科分类—自然科学总论 北京出版社《现代科技综述大辞典上》第34页(4066字)
研究实Banach空间(流形) 上实Frechet可微泛函数,即I∈C′(
上实Frechet可微泛函数,即I∈C′( ,R′)则I′(x)
,R′)则I′(x) ,而I′(x)=0是指〈I′(x),y〉(
,而I′(x)=0是指〈I′(x),y〉( ,
, )=0,
)=0, 。
。
称x为临界点相应的泛函值称为临界值。算子方程I′(x)=0与某个微分方程定解问题(称为所给泛函数的Euler方程)相对应。这时泛函数的临界点是定解问题的弱解,弱解的意义由泛函数所在空间和它的拓扑决定。由于它的应用背景广泛,临界点理论一直受到许多学者的注意。
临界点理论渊源于古典变分方法。后者把寻求泛函极值和极值点化为微分方程定解问题研究。
Dirichlet原理则是最早的例子,它反过来从极小化Dirichlet积分出发求解Laplace方程。直到19世纪末期,Poincare和Hilbert才给出了这个问题的完整叙述和证明。通常把寻求极小值点的方法称之为变分学中的直接方法。
它主要是求找泛函数的极小化叙列并研究它的收敛性。往往需要泛函数关于弱拓扑的下半连续性,这是Tonelli在20年代提出的。沿着这个方向还应提到凸分析的发展,Clarke和Ekeland的对偶(Duality)原理及Ekeland的变分原理。
临界点理论的发展可追溯到20世纪30年代。基于最速下降流(由初值问题 ,
, 定义)方法,Ljusternik-Schnirelman证明,定义在紧流形
定义)方法,Ljusternik-Schnirelman证明,定义在紧流形 上光滑实值函数I至少有Cat(
上光滑实值函数I至少有Cat( )个临界点在
)个临界点在 上;这里
上;这里 的畴数(Category)是指复盖区的,在
的畴数(Category)是指复盖区的,在 中可收缩闭子集的最小数目。
中可收缩闭子集的最小数目。
同一时期,Morse证明,当泛函数I非退化时,它的Morse指数为k的临界点个数不少于紧流形 的k阶贝蒂(Betti)数;这里I非退化是指在它的任一临界点
的k阶贝蒂(Betti)数;这里I非退化是指在它的任一临界点 处,它的Hessian矩阵I″(
处,它的Hessian矩阵I″( )非奇异,此时I″(
)非奇异,此时I″( )的最大负子空间维数记为临界点
)的最大负子空间维数记为临界点 的Morse指数。
的Morse指数。
他们从不同方面揭示了紧流形上函数的临界点集合与流形自身拓扑性质的关系并成功地应用到闭测地线和极小曲面问题得到多解。
20世纪60年代Palais-Smale推广他们的工作到无穷维Hilbert和Banach空间。他们提出描述泛函数紧性的(C)条件(现在称之为PS条件): ,若I(xn)有界且I′(xn)→0,则{xn}有收敛叙列。并且给出了伪梯度向量场概念:令
,若I(xn)有界且I′(xn)→0,则{xn}有收敛叙列。并且给出了伪梯度向量场概念:令 称V:
称V: 是I的伪梯度向量场,如果‖V(x)‖≤2‖I′(x)‖,<V(x),
是I的伪梯度向量场,如果‖V(x)‖≤2‖I′(x)‖,<V(x), 。当I∈C′(
。当I∈C′( ,|R′),他们证明此时V确实存在。利用它产生泛函数的下降流η:
,|R′),他们证明此时V确实存在。利用它产生泛函数的下降流η: ,由
,由 ,
, 定义。于是有
定义。于是有
Morse形变引理 设I∈C′( ,R)满足PS条件,
,R)满足PS条件, 是
是 的一个阾域。则存在ε>0使得
的一个阾域。则存在ε>0使得 。当
。当 ,
, 。
。
极小极大原理设I∈C1( ,R)满足PS条件。设Г是
,R)满足PS条件。设Г是 中集合族,关于下降流η不变:若集合B∈Г则η(t,B)∈Г,
中集合族,关于下降流η不变:若集合B∈Г则η(t,B)∈Г, [0,1],那么只要
[0,1],那么只要 有限。C必是I的临界值。
有限。C必是I的临界值。
取Г 为 中单点集,则
中单点集,则 。
。
特别它包含了Ljusternik-Schnirelmar的结果:令 ;
; ,则上述方式确定的Ck是临界值。
,则上述方式确定的Ck是临界值。
重数定理 如果C=Ck+1=…=Ck+n,则I至少有n个临界点在临界水平C。
自然它的前提是 有非平凡拓扑使Гk非空。当空间
有非平凡拓扑使Гk非空。当空间 有平凡拓扑,而泛函数在某紧群G作用下不变时,可考虑商空间
有平凡拓扑,而泛函数在某紧群G作用下不变时,可考虑商空间 上的泛函数,通常商空间有较丰富的拓扑。
上的泛函数,通常商空间有较丰富的拓扑。
但若群G不是自由作用,商空间将是奇异的,不再是流形,上述途径也行不通。另一方面畴数是个比较难计算的拓扑不变量。为此Coffman和Krasnosel′skii提出了亏格(genus)概念,给出了Z2群指标。80年代以后多种指标理论出现,大大扩充了变分理论的应用范围。
应该提到的有Fadell-Husseini-Rabinowity的上同调指标,Ambrosetti-Rabinowity的伪指标,Benci的S1群几何指标。
当空间拓扑平凡,泛函数又无对称性时,直至80年代Ambrosetti-Rabinowity给出了山路引理才打开了一个新局面。
山路引理(Mountain Pass Lemma) 设I∈C1( ,R)满足PS条件,且①I(0)=0,②存在ρ>0,α>0使I(x)≥α当‖x‖=ρ;③存在
,R)满足PS条件,且①I(0)=0,②存在ρ>0,α>0使I(x)≥α当‖x‖=ρ;③存在 ,‖e‖>ρ使I(e)<α,令Г={p∈C([0,1]
,‖e‖>ρ使I(e)<α,令Г={p∈C([0,1] ;p(0)=0,p(1)=e}。则
;p(0)=0,p(1)=e}。则 是临界值。
是临界值。
随后出现Ni(倪伟明)、Benci-Rabiowij提出的环绕(linking)概念,给出了泛函数在零点不定时的集合类Г。针对应用,出现了众多的变分原则,它们与硬分析技巧相结合大大地扩充了应用范围。
Morse理论主要是通过水平集Ia和泛函数I在集合I-1([a,b])中临界点集的构造来描述水平集Ib的构造。它的基础是Morse引理:Morse函数(即它的所有临界点非退化)在临界点附近局部微分同胚于一个标准的非退化的,保持Morse指数的二次函数。
因而泛函数在这点附近的行为可以用一系列同调群(临界群)来刻划:设U是x0的领域且x0是U中I的唯一临界点,对应于临值c。令 ,I-1{c}\{x0}∩U,Q),q=0,1,…,其中Q是系数群。
,I-1{c}\{x0}∩U,Q),q=0,1,…,其中Q是系数群。
称它们为I在x0的临界群。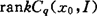 称为I在x0的Morse型数。
称为I在x0的Morse型数。
当I∈C2,x0是Morse指数为j的非退化临界点,有

Morse不等式设I∈C1( ,R)满足PS条件,设a<b是I的正则值,I在I-1[a,b]上至多有有穷个临界值c1<c2<…cm,每个临界点的临界群都是有穷秩的。记
,R)满足PS条件,设a<b是I的正则值,I在I-1[a,b]上至多有有穷个临界值c1<c2<…cm,每个临界点的临界群都是有穷秩的。记 Icj-cj,Q),
Icj-cj,Q), 。
。
则
 且
且 。
。
胞腔粘合定理 设I∈C2( ,R)满足PS条件。
,R)满足PS条件。
又设c是它的孤立临界值, 都是非退化临界点,则存在ε>0,使
都是非退化临界点,则存在ε>0,使 与
与 有相同伦型,这里Ic-i∩hi(Bmi)=I-1{c-ε}∩h,
有相同伦型,这里Ic-i∩hi(Bmi)=I-1{c-ε}∩h, ,
, ,mi是yi的Morse指数,Bmi是mi维球,
,mi是yi的Morse指数,Bmi是mi维球, 是同胚映射,
是同胚映射, 对应I″(zi)的极大负不变子空间,而
对应I″(zi)的极大负不变子空间,而 ,
, ,hi(θ)=zi,i=1,…,l,
,hi(θ)=zi,i=1,…,l,
这里要求函数非退化。它不仅在理论上是个限制,在应用上也是很难先验知道的。
70年代Gromall-Meyer利用伪梯度向量场建立了孤立临界点的G-M对(pair)(或称管状领域),除去了非退化假设。这种思想被conley进一步发展,建立了孤立临界块的Morse指标,它甚致能处理非变分问题。
这里还应提到Rothe50年代的工作。
Morse理论提供了多临界点存在的信息。在某些情形它比Ljusternik-Schnirelman理论给出更好的估计。张恭庆研究二者的关系,确定由极小极大原理得到的临界点的临界群,拓扑度,从而给出更精确的估计为判定多解提供更多的信息。
这方面工作还可见Hofer、刘嘉荃、田刚、Solimini等的研究成果。
临界点理论的应用自始至终伴随着它发展,在研究几何学、物理学中提出的非线性椭圆边值问题,非线性波动方程周期解,Hamilton方程组周期轨道递等问题上得到许多新的有意义的结果,近年来大量工作关心“失去紧性”问题,即PS条件不是整体满足时,如何挖掘出问题的紧性,由于PS条件破坏的水平集值有着物理学或几何学意义,相信这也将是近期研究工作的热点。
例如几何学中Yamabe问题引出的临界指数问题:这方面工作可见Schocn,Brezyis-Nirenberg、siruwe、Bahri、Coron和丁伟岳的研究等。
由天体力学三体问题等为背景的奇异位势Hamil ton系统非碰撞轨道的存在性可见Moser、Ambrosetti、Coti Zelati等的论着。
特别在研究Hamilton系统时,Conley-Zehnder、Floer关于Arnold猜测的结果:用辛几何研究Weinstein猜测的工作可见Viterbo、Hofer,Zehnder和龙以明等的工作。
。【参考文献】:
1 Palais R S. Proc Symp Pure Math. AMS Provi -dence, 1970,15:185~212
2 Rabinowitz P H. Minimax methods in critical point theory with applications to differential equations. CBS,1986,No. 65
3 NirenbergL. Bull AMS(New Ser) ,1981,4:267~302
4 Kung -ching chang. Infinite dimensional Morse theory and applications. Monceeial ,canads .1985
6 Struwe M.Variational Methods,Springer-Verlag,1990
(浙江大学吴绍平教授撰)