测量误差的分类
出处:按学科分类—工业技术 中国建材工业出版社《工程测量实用技术手册》第93页(1831字)
观测误差按其性质,可分为系统误差、偶然误差和粗差。
1.系统误差
系统误差是由仪器制造或校正不完善、观测员生理习性、测量时外界条件、仪器检定时不一致等原因引起的。在同一条件下获得的观测列中,其数据、符号,或保持不变,或按一定的规律变化。系统误差在观测成果中具有累计性,对成果质量影响显着,应在观测中采取相应措施予以消除。
2.偶然误差
偶然误差的产生取决于观测进行中的一系列不可能严格控制的因素(如湿度、温度、空气振动等)的随机扰动。在同一条件下获得的观测列中,其数值、符号不定,表面看没有规律性,实际上是服从一定的统计规律的。随机误差又可分两种:
1)误差的数学期望不为零,称为随机性系统误差。
2)误差的数学期望为零,称为偶然误差。
这两种随机误差经常同时发生,需根据最小二乘法原理加以处理。
3.粗差
粗差是指由一些不确定因素引起的误差。国内外学者在粗差的认识上还未有统一的看法,目前的观点主要有以下几类:
1)将粗差看作与偶然误差具有相同的方差,但期望值不同。
2)将粗差看作与偶然误差具有相同的期望值,但其方差相差巨大。
3)认为偶然误差与粗差具有相同的统计性质,但有正态与病态的不同。
以上的理论均是建立在把偶然误差和粗差均看作是属于连续型随机变量的范畴。还有一些学者认为粗差属于离散型随机变量。
当观测值中剔除了粗差,排除了系统误差的影响,或者与偶然误差相比系统误差处于次要地位后,占主导地位的偶然误差就成了研究的主要对象。从单个偶然误差来看,其出现的符号和大小没有一定的规律性,但对大量的偶然误差进行统计分析,就能发现其规律性,误差个数越多,规律性越明显。
例如,在相同的观测条件下,对358个三角形的内角进行了观测。由于观测值含有偶然误差,致使每个三角形的内角和不等于180°。设三角形内角和的真值为X,观测值为L,其观测值与真值之差为真误差△,用下式表示为:
△=Li-X (i=1,2,…,358)
由上式计算出358个三角形内角和的真误差,并取误差区间为0.2″,以误差的大小和正负号分别统计出它们在各误差区间内的个数V和频率V/n,结果列于表6-1中。
表6-1 偶然误差的区间分布
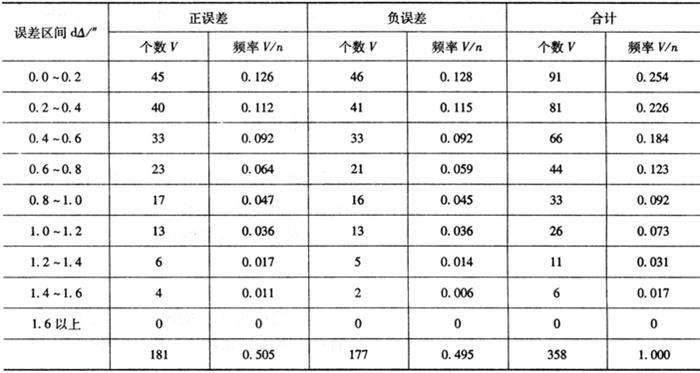
从表6-1中可看出,最大误差不超过1.6″,小误差比大误差出现的频率高,绝对值相等的正、负误差出现的个数近于相等。通过大量实验统计结果证明了偶然误差具有如下特性:
1)在一定的观测条件下,偶然误差的绝对值不会超过一定的限度。
2)绝对值小的误差比绝对值大的误差出现的可能性大。
3)绝对值相等的正误差与负误差出现的机会相等。
4)当观测次数无限增多时,偶然误差的算术平均值趋近于零,即
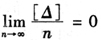
上述第四个特性说明,偶然误差具有抵偿性,它是由第三个特性导出的。
掌握了偶然误差的特性,就能根据带有偶然误差的观测值求出未知量的最可靠值,并衡量其精度。同时,也可应用误差理论来研究最合理的测量工作方案和观测方法。