集成运算放大电路

出处：按学科分类—工业技术 江苏科学技术出版社《简明电工计算手册》第248页（11328字）

集成运算放大器实际上是一种高电压增益、高输入电阻和低输出电阻的直接耦合的多级放大电路。由于在发展初期主要用于模拟电子计算机中实现数字运算，故称运算放大器。由于线性集成电路首先用作运算放大器，所以习惯上仍称线性集成电路为集成运算放大器。

集成运算放大器通常由输入级、中间级、输出级和偏置电路四部分组成。

输入级对其要求是输入电阻高、能减小零点漂移和抑制干扰信号，一般由具有恒流源的差动放大电路组成。

中间级主要进行电压放大，要求其电压放大倍数高，一般由共发射极放大电路组成。

输出级与负载相接，要求其输出电阻低，带负载能力强，通常由射极输出器或互补对称电路组成。

为便于分析，通常把集成运算放大器理想化，理想化的条件是：开环电压放大倍数无穷大，开环输入电阻无穷大，输出电阻为零，输入失调电压、输入失调电流及它们的漂移均为零，共模抑制比无穷大。

理想运算放大器两输入端的电位之差为零，两输入端的电流也为零。同时引入虚短、虚地、虚断概念便于对运算放大器进行分析。

集成运算放大器的种类较多，通常可分为信号运算、信号滤波、信号发生等电路形式。

1．信号运算电路的计算

(1)反相输入比例运算放大器

图3－29为反相输入比例运算放大器。输入信号u₁经电阻R₁加在反相输入端，同相输入端经电阻R₂接地，R₂为平衡电阻，以保证放大器输入级差动放大电路的对称性，输出信号经反馈电阻R_F反馈到反相输入端，形成一个深度的电压并联负反馈。只要反馈电阻R_F和输入回路电阻R₁本身阻值准确和稳定，便可得到准确的比例运算。其运算关系为：

图3—29 反相输入放大器

式中 A_uf——闭环电压放大倍数；

u_o——输出电压(V)；

u₁——输入电压(V)；

R_F——反馈电阻(Ω)；

R₁——输入回路电阻(Ω)；

R₂——平衡电阻(Ω)；

R_1f——闭环输入电阻(Ω)；

R_of——闭环输出电阻(Ω)。

(2)同相输入比例运算放大器

图3－30为同相输入比例运算放大器。输入信号u₁经平衡电阻R₂加在同相输入端，输出信号经反馈电阻R_F反馈到反相输入端，输出电压与输入电压同相位，相当于引入了电压串联负反馈。输出电压与输入电压的幅度成正比，实现了同相比例运算。其运算关系为：

图3－30 同相输入放大器

式中 A_uf——闭环电压放大倍数；

u_o——输出电压(V)；

u₁——输入电压(V)；

R_F——反馈电阻(Ω)；

R₁——输入回路电阻(Ω)；

R₂——平衡电阻(Ω)；

R_1f——闭环输入电阻(Ω)；

R_of——闭环输出电阻(Ω)。

(3)差动输入比例运算放大器

图3－31为差动输入比例运算放大器。输入信号u₁₁和u₁₂分别通过电阻R₁和R₂在放大器的反相输入端和同相输入端，输出电压将与此两个输入信之差成比例，故称为差动输入比例运算放大器。实质上差动输入比例运算放大器是由反相输入和同相输入两种运算放大器组合而成。其运算关系为：

图3－31 差动输入运算放大器

①u₁₁=0，u₁₂作用时，为同相输入比例运算放大器。其输出电压为：

为保持输入端平衡，应使R₁=R₂、R₃=R_F，则输出电压u_o2为：

②u₁₂=0，u₁₁作用时，为反相输入比例运算放大器。其输出电压为：

③u₁₁和u₁₂同时作用时，其输出电压为：

差动输入比例运算放大器可作为减法器。当u₁₂＞u₁₁时，u_o为正值；当u₁₂＜u₁₁时，u_o为负值。

式中 u_o——输出电压(V)；

u_o2——同相输入时的输出电压(V)；

u_o1——反相输入时的输出电压(V)；

u₁₁，u₁₂——输入电压(V)；

R_F——反馈电阻(Ω)；

R₁、R₂、R₃——输入回路电阻(Ω)；

A_uf——闭环电压放大倍数；

R_1f——闭环输入电阻(Ω)；

R_of——闭环输出电阻(Ω)。

(4)反相加法运算放大器

图3－32为反相加法运算放大器。反相加法运算放大器是在反相输入比例运算放大器的基础上增加多个输入支路，把输入电压u₁₁、u₁₂、u₁₃通过电阻R₁、R₂、R₃转换成输入电流i₁、i₂、i₃，利用虚地概念可得出其运算关系为：

图3－32 反相加法器

若 R_F=R₁=R₂=…=R_n，则

u_o=－(u₁₁+u₁₂+…+u_1n) (3－167)

R=R₁∥R₂∥R₃∥R_F (3－168)

式中 u_o——输出电压(V)；

u₁₁，u₁₂，u₁₃——输入电压(V)；

i₁，i₂，i₃——输入电流(A)；

i_f——反馈电流(A)；

R_F——反馈电阻(Ω)；

R₁、R₂、R₃——输入回路电阻(Ω)；

R——平衡电阻(Ω)。

(5)同相加法器

图3－33为同相加法运算放大器。同相加法运算放大器是在同相输入比例运算放大器的基础上增加多个输入支路，把输入电压u₁₁、u₁₂、u₁₃通过电阻R₁、R₂、R₃转换成输入电流i₁、i₂、i₃，利用虚短、虚断概念，可得出其运算关系为：

图3－33 同相加法器

R′=R₁∥R₂∥R₃∥R (3－170)

电阻配接应满足平衡要求：

R₁∥R₂∥R₃∥R=R₄∥R_F (3－171)

式中 u_o——输出电压(V)；

u₁₁、u₁₂、u₁₃——输入电压(V)；

R_F——反馈电阻(Ω)；

R₁、R₂、R₃、R₄、R——输入回路电阻。

［例3－12］ 在图3－32所示的反相加法运算放大器中，已知R₁=R₂=R₃=6kΩ，R_F=120kΩ，u₁₁=u₁₂=u₁₃=0．3mV。求输出电压u_o和平衡电阻R的值。

［解］ 输出电压

(6)积分运算放大器

图3－34为积分运算放大器。把反相输入比例运算放大器中的反馈电阻用反馈电容C_F替代，就构成了积分运算放大器。其计算关系为：

图3－34 积分运算放大器

若输入电压u₁为恒定值U₁，则输出电压可表示为：

式中 u_o——输出电压(V)；

u₁——输入电压(V)；

u_o0——输出电压初始值(V)；

R₁——输入回路电阻(Ω)；

C_F——积分电容(F)。

输出电压随时间t而线性变化。

(7)微分运算放大器

图3－35为微分运算放大器。将图3－34所示积分运算放大器中的电阻R₁和反馈电容C_F调换位置，就构成了微分运算放大器。

其计算关系为

图3－35 微分运算放大器

即输出电压u_o与输入电压u₁对时间的一次微分值成正比，且极性相反。

式中 u_o——输出电压(V)；

u₁——输入电压(V)；

R_F——反馈电阻(Ω)；

C₁——微分电容(F)；

t——时间(s)。

(8)对数运算放大器

图3－36为对数运算放大器。将反相输入比例运算放大器中的反馈电阻换成半导体二极管或双极型三极管，就构成了对数运算放大器。对数运算放大器的输出电压是输入电压的对数函数。其运算关系为：

图3－36 对数运算放大器

式中 u_o——输出电压(V)；

u₁——输入电压(V)；

U_T——温度电压当量，室温27℃时；U_T≈26(mV)；

I_SR——PN结反向饱和电流(A)；

R₁——输入回路电阻(Ω)。

(9)指数运算放大器

图3－37为指数运算放大器。将图3－36所示对数运算放大器中的电阻R₁和三极管V的位置对调，就构成了指数运算放大器。反对数运算放大器的输出电压是输入电压的指数函数。

其运算关系为：

图3－37 指数运算放大器 (3－176)

式中 u_o——输出电压(V)；

u₁——输入电压(V)；

U_T——温度电压当量，室温27℃时，U_T≈26(mV)；

I_SR——PN反向饱和电流(A)；

R_F——反馈电阻(Ω)。

(10)乘法运算放大器

图3－38为乘法运算放大器。利用对数运算放大器和加法运算放大器相结合，就可构成乘法运算放大器。其运算关系为：

图3－38 乘法运算放大器

式中 u_o——输出电压(V)；

u₁₁、u₁₂——输入电压(V)；

R_F——反馈电阻(Ω)；

R₁、R₃——输入回路电阻(Ω)；

I_SR1、I_SR2、I_SR3——PN结反向饱和电流(A)。

2．信号滤波电路的计算

滤波器是一种选频电路，它能使指定频率范围内的信号顺利通过；而对其他频率的信号加以抑制，使其衰减很大。

滤波电路通常根据信号通过的频带来命名。

低通滤波电路(LPF)——允许低频信号通过，将高频信号衰减；

高通滤波电路(HPF)——允许高频信号通过，将低频信号衰减；

带通滤波电路(BPF)——允许某一频段内的信号通过，将此频段之外的信号衰减；

带阻滤波电路(BEF)——阻止某一频段内的信号通过，而允许此频段之外的信号通过；

全通滤波电路(APF)——没有阻带，信号全通，但相位变化。

对于幅频响应，通常把能够通过的信号频率范围定义为通带，而把受阻或衰减的信号频率范围称为阻带，通带和阻带的界限频率叫做截止频率。

(1)低通滤波电路的有关计算

图3－39为简单一阶低通滤波电路。电路中R₁和C_F组成低通网络，低频信号经电阻R₁及运放反相输入端输入，而高频信号被并联在反馈电阻R_F上的滤波电容C_F旁路掉了，因电容有隔直通交的特点。低通滤波电路的有关计算为：

图3－39 简单一阶低通滤波电路

截止频率

平衡电阻

R₂=R₁∥R_F (3－179)

式中 f_p——截止频率(Hz)；

C_F——滤波电容(F)；

R_F——反馈电阻(Ω)；

R₁——输入回路电阻(Ω)；

R₂——平衡电阻(Ω)。

(2)高通滤波电路的有关计算

图3－40为简单一阶高通滤波电路。电路中R₁和C₁组成高通网络，高频信号经电阻R₁，电容C₁及运放反相输入端输入，而低频信号则被电容C₁隔离。高通滤波电路的有关计算为：

图3－40 简单一阶高通滤波电路

截止频率

平衡电阻

R₂=R_F (3－181)

式中 f_p——截止频率(Hz)；

R_F——反馈电阻(Ω)；

R₁——输入回路电阻(Ω)；

R₂——平衡电阻(Ω)；

C₁——滤波电容(F)。

(3)带通滤波电路的有关计算

图3－41为二阶带通滤波电路。电路中电阻R₁和电容C组成低通网络，电阻R₂和电容C组成高通网络，两者相串联就组成了带通滤波电路。带通滤波电路允许某一频段内的信号通过，将此频段之外的信号衰减。带通滤波电路的有关计算为：

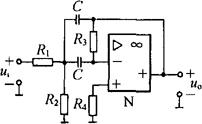
图3－41 二阶带通滤波电路

频带宽度：

中心点所对应的角频率：

中心频率

品质因数

式中 B——频带宽度(rad／s)；

ω₀——中心点所对应的角频率(rad／s)；

Q——品质因数；

R₁、R₂、R₃——滤波电阻(Ω)；

C——滤波电容(F)；

f₀——中心频率(Hz)。

(4)带阻滤波电路的有关计算

图3－42为二阶带阻滤波电路。从输入信号中减去带通滤波电路处理过的信号，就可得到带阻信号。带阻滤波电路由带通滤波电路和反相输入比例运算放大电路组合而成。带阻滤波电路阻止某一频段内的信号通过，而允许此频段之外的信号通过。带阻滤波电路常用于电子干扰系统。其频带宽度、中心点所对应的角频率及品质因数的计算与带通滤波电路的计算相同。

图3－42 二阶带阻滤波电路

频带宽度

中心点所对应的角频率：

中心频率

品质因数

电阻配接应满足平衡要求：

R₃=R₄，R₆=R_F1∥R_F2∥R₅ (3－189)

式中 B——频带宽度(rad／s)；

ω₀——中心点所对应的角频率(rad／s)；

Q——品质因数；

R₁、R₂、R₃——滤波电阻(Ω)；

R_F1、R_F2——反馈电阻(Ω)；

f₀——中心频率(Hz)；

R₄、R₅、R₆——输入回路电阻(Ω)；

C－—滤波电容(F)。

［例3－13］ 在图3－41所示的二阶带通滤波电路中，已知R₁=10kΩ，R₂=2kΩ，R₃=120kΩ，C=0．01μF。求中心点所对应的角频率ω₀、中心频率f₀、频带宽度B和品质因数Q。

［解］ 中心点所对应的角频率

中心频率

品质因数

3．信号发生电路的计算

波形发生电路又称信号源或振荡器。振荡器按波形分为正弦波和非正弦波振荡器两类。非正弦波振荡器可由比较器和RC电路组成。比较器是将运算放大器的反相输入端和同相输入端所输入的电压进行比较的电路。

在开环比较器中，引入适量的正反馈，可加速电路状态的转换，利用RC电路的充放电作用和运算放大器输出端的电压转换，就可以产生非正弦波，如矩形波、三角波、锯齿波等。

(1)正弦波发生器

图3－43为文氏电桥正弦波发生器。其振荡频率计算为：

图3－43 文氏电桥正弦波发生器

式中 f₀——振荡频率(Hz)；

R——选频电阻(Ω)；

C——选频电容(F)；

R_F——反馈电阻(Ω)；

R₁——输入回路电阻(Ω)。

(2)方波和三角波发生器

图3－44为方波和三角波发生器。将方波信号输入到积分运算放大器，其输出可得三角波形信号，将三角波信号输入到比较器，其输出可得方波信号。用同相滞回比较器和反相积分电路互相联接，就可构成方波和三角波发生器。其振荡频率为：

(a)电路

(b)波形

图3－44 方波和三角波发生器

式中 f₀——振荡频率(Hz)；

n_w——电阻R_w的分压系数；

R₁、R₃——输入回路电阻(Ω)；

R_f——反馈电阻(Ω)；

C_f——积分电容(F)。

(3)锯齿波发生器

图3－45为锯齿波发生器。当积分电路正向积分的时间常数大于反向积分的时间常数，或者反向积分的时间常数远大于正向积分的时间常数，那么输出电压u_o上升和下降的斜率相差很多，就可以获得锯齿波。利用二极管的单相导电性使积分电路两个方向的积分通路不同，就可构成锯齿波发生器。锯齿波、正弦波、方波、三角波是常用的基本测试信号。在示波器中，锯齿波发生器作为时基扫描电路。其振荡频率的计算为：

(a)电路

(b)波形

图3－45 锯齿波发生器

式中 f₀——振荡频率(Hz)；

n_w——电阻R_w的分压系数；

R₁、R₃、R₆——输入回路电阻(Ω)；

R_f——反馈电阻(Ω)；

C_f——积分电容(F)。

［例3－14］ 在图3－44所示的方波和三角波发生器电路中，已知R₁=10kΩ，R₃=120kΩ，R_f=20kΩ，C_f=0．2μF，n_w=0．8。求方波和三角波发生器的振荡频率。

［解］ 振荡频率