圆柱及相贯体的展开
出处:按学科分类—工业技术 江苏科学技术出版社《铆工实用技术手册》第171页(15632字)
圆柱面构件的展开下料是钣金工作者在施工中经常遇到的。此类构件在制造中一般可分为钢板卷制和成品钢管两种。因钢管有皮厚存在,所以在实际施工中有中径、内径、外径的分别,就是在展开中要使用其中的一个直径去放样和展开,也可能是用其中的一个直径去展开而用另一个直径去放样和求素线实长。这要根据构件的施工图样和施工要求去决定。但在一般情况下,钢板卷制的钢管在展开下料时都是以中径乘以π为周长展开长度。成品管一般是在下料时用样板围在外壁上画线,所以现场施工中均是以(外径+样板厚度)乘以π为周长展开长度来做样板。现场多习惯用油毡做样板而厚度多在2mm左右,所以一般取(外径+2mm)×π为圆管展开周长。本章中所有圆柱面展开时,无论放样计算时是内径或外径而展开周长均是用上述方法计算而不再说明。在实际施工时操作者可根据自己所使用的样板材料取厚度值。
1.被平面斜截后的圆柱管构件
圆柱面被平面斜截后的截面形状是平面椭圆,而被斜截后的圆柱面椭圆截面的展开线是以圆柱展开周长为周期,以截面在轴线位置上r为振幅的正弦曲线,如图3-49所示。

图3-49 圆柱面被平面斜截后的展开图
这种形体的展开只要求出截面与圆柱轴线垂面的夹角后就可用计算公式程编计算展开,如能熟练掌握程编运算过程,此种方法应是圆柱管构件展开中最实用而又快速准确的展开方法。
(1)通用计算公式
被平面斜截圆柱管的展开计算通用公式:

式中 xn——圆周ln值对应素线实长值;
α——截面和圆柱管轴线的垂面间的夹角;
L——截面和圆柱管轴线的垂面的交线到圆柱管轴线的距离;
R——圆柱管放样图半径;
r——圆柱管展开图半径;
ln——圆周展开长度、运算变量(0~2πr)。
此公式通用于圆柱管被平面斜截后各种构件中这种形体的展开,对于放样半径和展开半径是否相同都不必考虑,直接套用公式就可计算圆周展开的各素线实长值。而且在计算时直接用ln=πr或 的值输入运算就可得出半圆周和2/3圆周等中心线位置的素线实长值,使作图十分方便。公式示意如图3-50所示。
的值输入运算就可得出半圆周和2/3圆周等中心线位置的素线实长值,使作图十分方便。公式示意如图3-50所示。

图3-50 平面斜截圆柱管的展开示意图
(2)专用计算公式
上述通用计算公式一般可以适合这种形体在各种构件中的展开计算,在展开运算时不必考虑放样半径和展开半径的不同会在做展开图时带来错误,尤其对施工中习惯求出圆周展开时4个中心线的位置也十分方便。但在一般展开书籍和现场施工中仍习惯用等分圆周或等分角度的作法,所以对这两种作法也列出计算公式,供读者参考。而且它们也只是前面公式的演变,也较适合特殊情况的使用,我们将在后面的例题中讨论。公式示意如图3-51所示。

图3-51 平面斜截圆柱管的展开示意图
①斜截圆柱管的圆周等分展开计算公式:

式中 xn——圆周nx等分点对应素线实长值;
α——截面和圆柱管轴线的垂面间夹角;
L——截面和圆柱管轴线的垂面的交线到圆柱管轴线的距离;
R——圆柱管放样图半径;
n——圆柱管半圆周等分数;
nx——等分变量(0~2n)。
此公式计算展开用周长等分点距离应和展开计算时的等分相同,其计算公式是:

式中 ln——圆周等分数nx对应展开长度;
r——圆柱管展开图用半径;
n——圆柱管半圆周等分数;
nx——等分变量(0~2n)。
②斜截圆柱管的角度等分展开计算公式:
xn=tanα(L-R cosΦn)
式中 xn——°角度Φn等分对应素线实长值;
α——截面和圆柱管轴线的垂面间夹角;
L——截面和圆柱管轴线的垂面的交线到圆柱管轴线的距离;
R——圆柱管放样图半径;
Φn——圆心角等分变量(0°~360°)。
此公式计算用圆心角值在展开计算时应对应相同,其计算公式是:

式中 ln——圆周与圆心角Φn对应展开长度;
r——圆柱管展开图用半径;
Φn——圆心角等分变量(0°~360°)。
【例1】 两节直角圆管弯头
弯头是圆柱体管件中常见的构件。用圆管制造弯头一般是由多节组成的,而每节圆管又可以是钢板卷制或成品管两种。弯头展开放样中必须考虑相贯线的板厚关系。图3-52所示为钢板卷制的两节直角圆管弯头。

图3-52 两节直角圆管弯头
①用图解法展开。此构件在接点A处是内壁相交,在接点B处是外壁相交,所以须以接点A的内壁点和接点B的外壁点至圆管中心点为基准来作弯头展开曲线,因此圆管放样图分别各以D/2和D/2-δ为半径来作图,如图3-53所示。因为直角弯头构件的两节圆管完全相同,所以仅做一节圆管的展开就可以了。

图3-53 两节直角圆管弯头的放样展开图
此构件用平行线法展开。将两个半圆在平面图中各作六等份得1、2、3…6、7各点,由各点上引轴线的平行线交相贯线得1′、2′、3′…6′、7′各点,沿正视图底边作水平线,在线上截取线段等于展开周长π(D-δ),并12等分,过各等分点作垂线与过1′、2′、3′…6′、7′所做水平线交于1″、2″、3″…6″、7″各点。光滑连接各点即得到构件的全部展开图形。
②用程编计算公式法展开。为便于说明展开方法我们将构件代入具体数值。
如图3-52所示,D=1000mm,δ=10mm,H=1000mm,n=16,采用下述公式计算。

式中 α=45°;
L=Htanα=1000mm×tan45°=1000mm,

将以上数据代入公式得:


因构件展开图形是对称图形,所以只要做半圆周16等分展开计算就可以做出全部展开图形。为了作展开图时的方便,根据ln的值可做出32等分的全部展开图形,同时也可输入nx的几个等分点对xn的值进行检验或全部算出,因程编运算可十分方便地得出结果,故使作展开图形时更加方便。现将上面三个计算式进行程编运算,所得结果见表3-10。
表3-10 两节直角圆管弯头的展开计算值


展开图形作法:取线段长度为3110.2,并将线段按表3-10中ln的数值进行32等分取点,过各点作线段的垂线,在各垂线上按表3-10中32等分的各对应xn值取点,然后光滑连接各点就可得到全部展开图,如图3-54所示。

图3-54 两节直角圆管弯头的计算展开图
圆管的展开等分数一般施工中以50~100作等分较合适。图解法展开时,为使图线清楚一般采用12等分,实际施工时可根据管径大小来决定等分数。
【例2】 平面任意角度三节圆管弯头
图3-55所示为任意角度三节圆管弯头的投影图。

(a)

(b)
图3-55 任意角度三节弯头
(a)正视图;(b)放样展开图
两端节较长,中节较短。但如将β角4等分即得到4个相同的部分,只要展开其中的一个部分,然后对称作图就可得到中节的展开,加上直管部分就可得到两端圆管的展开。本例如用钢板卷制双面坡口形式时,放样图半径和展开图半径就都是应用圆管的中径去展开作图或计算作图。
①用图解法展开。此构件的展开放样图用中径画出。如图3-55(b)所示,用平行线法展开。
作角度等于β角并将其四等分,在中心等分线上从圆心截取H长度得点A。过A点作垂线,即为中节圆管的轴线。在轴线两侧(D-δ)/2距离处作轴线的平行线交相邻两角平分线,即得到中节的放样正视图,沿轴线作出圆管的俯视图,将俯视图中的圆周12等分,过各等分点作圆管的素线和相贯线交于1、2、3…6、7各点,将中心角平分线延长截取线段长度为圆管中径展开长度并且12等分,过各等分点作垂线与相贯线上过1、2、3……各点作水平线交于1′、2′、3′……各点,光滑连接各点即可得到相贯线的展开曲线。对称作图就得到中节的全部展开图形。作展开图形时为错开相贯线处的丁字焊缝和下料时节省材料,接缝位置一般选在如图3-55中4线的位置。但这样下料后在制造中就要注意正曲和反曲的不同,下料时应注明正反曲面,以防止十字焊缝的出现。
②用程编计算公式法展开。为便于计算,我们在构件中代入具体数值。如图3-55(a)所示,设D=820mm、δ=20mm、H=1600mm、β=75°,选用展开计算通用公式:


为作图的方便将素线实长值编序号并以ln为变量代入计算式程编计算,结果见表3-11。
表3-11 任意角度三节圆管弯头展开计算值

表3-11中 的值为628.3mm,πr的值为1256.6mm,这两值在程编计算时可直接代入并求出以便在作展开图时使用。
的值为628.3mm,πr的值为1256.6mm,这两值在程编计算时可直接代入并求出以便在作展开图时使用。
展开图作法:如图3-56所示。取线段长度等于2πr,将线段按表3-11中ln的值进行等分。等分时将8线作为接缝位置,因是对称图形,表中仅列出半圆周展开值。过各等分点作线段的垂线,在垂线上线段两面各按ln对应的xn值取点并将各点光滑连接,即得到中节的全部展开图形。

图3-56 任意角度三节弯头的计算展开图
【例3】 四节圆管弯头
图3-57为四节圆管弯头的投影图。

图3-57 四节圆管弯头
本例用程编计算公式法展开。
①形体分析:和三节弯头相同,如果将90°角分为6等分,即得到6个相同的圆管部分,只要计算作出一部分的展开图就可得到全部的展开图。设D=377mm、δ=10mm、H=350mm,已知90°,6等分后每等份为15°。此圆管件因焊接的条件要求结合处均作外坡口处理,这样结合处就均是内壁接触,所以放样图半径即应是R=178.5mm,而如用成品管制造时画线样板的展开半径即应是r=189.5mm。并且展开是对称图形,作半圆周展开计算即可。
②作计算和展开用草图,如图3-58所示,为提高展开精确度,计算时半圆周作12等分计算,而在样板制作时可根据曲线情况选用。展开计算用等分作图的计算公式。

图3-58 四节圆管弯头计算放样草图
③选用展开计算公式。

式中已知:α=15°,L=H=350mm,R=178.5mm,r=189.5mm,n=12。

以nx为变量程编计算得到的xn和ln的对应计算值见表3-12。
表3-12 四节圆管弯头展开计算值

④圆管画线样板作法:如图3-59取线段长等于595.3mm,在线段上作12等分。过各等分点作线段的垂线,在各垂线上分别截取xn所对应的ln的值的长度得各点。光滑连接各点即得到半圆周的展开曲线,对称作图就可得到半节圆管的展开画线样板。再对称作图就可得到中间节的展开画线整体样板,如图3-59所示。

图3-59 四节弯头中节画线样板的计算展开图
【例4】 等径裤形圆柱三通管
图3-60是等径裤形圆柱三通管的投影图和展开图。构件由五节直径相同的圆柱管构成,结构左、右对称。上三节管的轴线交于一点,且两两间夹角相等。各管间的结合线均为平面曲线,正面投影积聚为直线。构件的已知尺寸为D=210,H=170,L=210,H1=130,t=3,计算展开数据。

图3-60 等径裤形圆柱三通管
①计算方法:

式中:n——展开时的圆周等分数量。
②计算展开数据:
取n=12,则等分角度 的计算增量为
的计算增量为 。
。
E=3.1415926×(210-3)=650.31

f0=60.62×cos0°=60.62
f1=60.62×cos30°=52.50
f2=60.62×cos60°=30.31
f3=60.62×cos90°=0
f4=-58.89×cos120°=29.45
f5=-58.89×cos150°=51.00
f6=-58.89×cos180°=58.89
由上面尺寸,运用平行线法可画出构件各节的展开图。
【例5】 带斜插管的等径圆柱三通管
图3-61为带斜插管的等径圆柱三通管的投影图和展开图。构件在四节直角等径圆柱弯管的基础上斜插一等径圆柱管,各管间的结合线均为平面曲线,正面投影积聚为直线。构件的已知尺寸为D=250,L=365,R=480,计算展开数据。

图3-61 带斜插管的等径圆柱三通管
①计算方法

H1=R·tan15° H=2H1

式中 n——圆管端口圆周等分数量。
②计算展开数据:

E=3.1415926×250=785.40

H1=480×tan15°=128.62
H=2×128.62=257.24


l0=0.134×250=33.5
l1=0.1238×250=30.95
l2=0.0947×250=23.68
l3=0.0513×250=12.83
根据以上数据,运用平行线法可画出构件的展开图。
【例6】 四节等径直角双向圆柱三通管
图3-62是四节等径直角双向圆柱三通管的投影图和展开图。它由左、右对称的两个四节直角圆柱弯管结合而成,各节间的结合线为平面曲线,其正面投影积聚为直线。构件的已知尺寸为D=1700,R=2800。因构件左、右对称,故只展开Ⅰ、Ⅱ、Ⅲ和Ⅳ节管,展开时为节省原料,先将Ⅱ、Ⅲ两节圆柱管绕其自身轴线旋转180°后,再与Ⅰ、Ⅲ两节拼接在一起,作整体展开。

图3-62 四节等径直角双向圆柱三通管
①计算方法

H1=R·tan15° H=2H1

式中 n——圆管端口圆周等分数量。
②计算展开数据:
取n=12,等分角度αi的计算增量为 。
。
E=3.1415926×1700=5340.71

H1=2800×tan15°=750.26
H=2×750.26=1500.52

根据以上数据,由平行线法可绘出各节的展开图。
【例7】 等径Y型补料圆柱三通管
图3-63是等径Y形补料圆柱三通管的投影图和展开图。下部两斜管轴线互相垂直,两管间夹有一等径圆柱面补料。各管间的结合线均为平面曲线,其正面投影积聚为直线。构件的已知尺寸为D=250,H=180,H1=305,H2=110,计算展开数据。

图3-63 等径Y形补料圆柱三通管
①计算方法

式中 n——展开时圆管圆周等分数量;
αi——展开时的等分角度。
②计算展开数据:
取n=12,则等分角度αi的计算增量为 。
。
E=3.1415926×250=785.4

α=305-110=195

f0=51.78×cos0°=51.78
f1=51.78×cos30°=44.82
f2=51.78×cos60°=25.89
f3=51.78×cos90°=0
根据以上数据,运用平行线法可画出各管和补料的展开图。
【例8】 等径补料圆柱三通管
图3-64是等径补料圆柱三通管的投影图和展开图。构件由三节轴线相交、且两两间夹角相等的圆柱主管及它们间的三块等径圆柱面补料构成,各结合线均为平面曲线,正面投影成直线。构件的已知尺寸为D=220,H=305,H1=140,计算展开数据。由于构件的对称性,只展开一节主管和一块补料即可。

图3-64 等径补料圆柱三通管
①计算方法:

式中 n——展开时圆管圆周等分数量;
αi——展开时的等分角度。
②计算展开数据:
取n=12,则等分角度αi的计算增量为 。
。
E=3.1415926×220=691.15

α=305-140=165

由以上数据,用平行线法可绘出主管和补料的展开图。
【例9】 等径正交补料圆柱三通管
图3-65是等径正交补料圆柱三通管的投影图和展开图。在竖直与水平圆柱管之间,有两块等径圆柱面补料。各表面间的结合线均为平面曲线,正面投影为直线。构件的已知尺寸为D=205,H=305,H1=150,L=610,L1=310,计算展开数据。

图3-65 等径正交补料圆柱三通管
①计算方法


式中 n——展开时圆管圆周等分数量;
αi、βi——展开时的等分角度。
②计算展开数据:
取n=12,则αi、βi的计算增量均为 。
。
E=3.1415926×205=644.03

b=305-150=155

f0=42.46×cos0°=42.46
f1=42.46×cos30°=36.77
f2=42.46×cos60°=21.23
f3=0
因为r1=r,所以有li=fi,i=0,1,2,3。
根据以上数据,运用平行线法可画出竖直、水平圆柱管和补料的展开图。
【例10】 丁字形等径补料圆柱三通管
图3-66是丁字形等径补料圆柱三通管的投影图和展开图。构件由水平、竖直圆柱管及它们间的等径圆柱面补料组成,它们间的结合线均为平面曲线,正面投影为直线。构件的已知尺寸为D=200,L=275,L1=120,H=510,H1=370,H2=90,计算展开数据。

图3-66 丁字形等径补料圆柱三通管
①计算方法:

a=L-L1 b=H1-H2

式中 n——展开时圆管圆周等分数量;
αi、βi、γi——展开时的等分角度。
②计算展开数据:
取n=12,则αi、βi和γi的计算增量均为 。
。
E=3.1415926×200=628.32

a=275-120=155
b=370-90=280


g0=58.94×cos0°=58.94
g1=58.94×cos30°=51.04
g2=58.94×cos60°=29.47
g3=58.94×cos90°=0
l0=25.83×cos0°=25.83
l1=25.83×cos30°=22.37
l2=25.83×cos60°=12.92
l3=25.83×cos90°=0
根据以上数据,运用平行线法可画出水平、竖直圆柱管及补料的展开图。
【例11】 带补料正交等径圆柱三通管
图3-67是带补料正交等径圆柱三通管的投影图和展开图。在竖直圆柱管和水平圆柱管之间,左、右有两块对称的补料,补料曲面为椭圆柱面的一部分,定位尺寸满足 。各部间的结合线均为平面曲线,正面投影为直线。构件的已知尺寸为D=200,H=290,L=510,H1=95,L1=60,计算展开数据。
。各部间的结合线均为平面曲线,正面投影为直线。构件的已知尺寸为D=200,H=290,L=510,H1=95,L1=60,计算展开数据。

图3-67 带补料正交等径圆柱三通管
①计算方法:


式中 n——展开时圆管圆周等分数量;
αi——圆管圆周等分角度。
②计算展开数据:
取n=12,则αi的计算增量均为 。
。
E=3.1415926×200=628.32

r=290-95=195
f0=195×cos0°=195
f1=195×cos30°=168.87
f2=195×cos60°=97.5
f3=195×cos90°=0

a1=134.35×cos30°=116.35
a2=134.35×cos60°=67.18
a3=134.35×cos90°=0


由计算所得参数,用平行线法可绘出竖直、水平圆管及补料的展开图。
【例12】 异径斜、偏交圆柱三通管
图3-68为异径斜、偏交圆柱三通管的投影图和展开图。主管与支管轴线倾斜且不相交,存在一定的偏距。两管的结合线为空间曲线,其正面投影积聚为圆弧。构件的已知尺寸有主管直径D=300,长度L=440,支管d=170、轴线长度H=320,两管轴线间倾斜角θ=60°、偏距e=50和尺寸L1=140,计算展开数据。

图3-68 异径斜、偏交圆柱三通管
①计算方法:


式中 n——支管管口圆周等分数量。
当θ=90°时,构件成为异径偏交圆柱三通管,接口的展开曲线形状对称,这时:
ai=-rcosφi i=0,1,…,n
bi=πRαi/180° i=0,1,…,n
fi=Rcos(αi-α0) i=0,1,…,n
②计算展开数据:
取n=12,则φi的计算增量均为 。
。
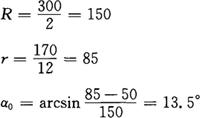
E=3.1415926×300=942.48
A=3.1415926×150×(90°-13.5°)/180°=200.28
E1=3.1415926×170=534.07

αi、ai、bi和fi(i=0,1,…,n)的数据见表3-13。
表3-13 异径斜、偏交圆柱三通管相关数据


若上例中,θ=90°,其他参数不变,αi、ai、bi和fi(i=0,1,2,…,n)的数据见表3-14。
表3-14

表中数据ai(i=0,1,…,12)由支管轴线定位尺寸L1右端为基准进行度量,其右侧为正,左侧为负。根据以上数据,可绘出主管及支管的展开图。
2.相贯体展开实例
(1)六棱柱与三棱柱相交展开(图3-69)

图3-69
(2)六棱柱与圆柱相交展开(一)(图3-70)

图3-70
(3)六棱柱与圆柱相交展开(二)(图3-71)

图3-71
(4)矩形棱柱与圆柱斜交展开(图3-72)

图3-72
(5)四棱柱与圆柱偏交展开(图3-73)

图3-73
(6)六棱柱与圆柱偏交展开(图3-74)

图3-74
(7)圆柱与圆柱斜交展开(图3-75)

图3-75
(8)圆球体的展开(图3-76)

图3-76
(9)六节三通管的展开(图3-77)

图3-77
(10)圆锥与圆锥斜交的展开(图3-78)

图3-78
(11)圆锥与圆柱相交的展开(图3-79)

图3-79
(12)和两斜面相接的斜截头圆锥的展开(图3-80)

图3-80
(13)匙的展开(图3-81)

图3-81
(14)坐浴浴盆的展开(图3-82)

图3-82
(15)圆锥与圆锥相交且同切一圆的展开(图3-83)

图3-83
(16)斜锥与角锥共底的展开(图3-84)

图3-84
(17)角锥与圆筒相交的展开(图3-85)

图3-85