相似设计的基本原理

出处：按学科分类—工业技术 企业管理出版社《工程师手册》第170页（4135字）

相似设计与相似方法一样，同样也是建立在相似理论的基础上。但相似设计中的“相似”概念更要全面些，所谓“相似”是指一组物理过程，其基本参数之间有固定比例的数量关系。因此，产品相似设计的关键在于如何找出相似系统各参数的相似比方程。

1．相似的条件

在讨论相似方法时，已初步建立了相似的概念，按照相似理论，物体的几何相似性，常能导致物理性能的相似性，这样，就可用缩小模型进行试验，以研究物体的物理性能，从而推断出实物所应具有的性能，或相似设计。

产品的模型试验中，不仅要求模型与原型做到几何相似，还要使试验中所包含的一切度量，如与运动有关的时间、速度、加速度、力等都必须相似。显然、物理相似的条件要比几何相似的条件复杂得多。满足物理相似的基本条件是：

(1)相似条件只能用于同类现象，即不仅要求现象的性质相同，还要求用同样的物理方程或函数关系来描述。

(2)两个物理现象相似，则参与描述该两现象的一切同名参数之间，在空间对应的各点上与在时间上相对应的瞬时都应互成比例。

具体说来，一组物理过程相似，则在相应时刻、相应参数之间比例关系，即相似比或相似系数C应保持为常数。写成公式即：

式中：q₁——原型的各种变量；

q₂——模型中与q₁相应的变量。

式中的变量不仅表示某一度量，也可以表示两个以上变量的积或商。如若模型与原型几何相似，并以L表示尺寸参数，按式(1)得长度的相似系数C_L为：

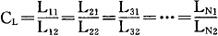
式中：L₁₁，L₂₁，L₃₁，…L_n1——原型各部分尺寸；

L₁₂，L₂₂，L₃₂，…L_n2——模型中对应于原型的各部分尺寸。

如原型与模型力相似，以P表示载荷，按式(1)则载荷的相似系数C_p为：

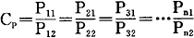
式中：P₁₁，P₂₁，P₃₁，…P_n1——原型承受的载荷；

P₁₂，P₂₂，P₃₂，…P_n1——模型中对应于原型各位置上所承受的载荷。

其余类推，如C_E为材料弹性模量相似比，C_M为扭矩相似比等等。

在SI单位制中，长度、力、时间为基本量纲。与此相对应，在相似比或相似系数的计算过程中，对互相独立的基本物理量：长度L、力F、时间T、温度C、电量Q等所形成的相似比就称为基本相似比。按量纲理论，某些参数的量纲由基本量纲导出，其相似比就称为导出相似比，如速度、加速度的相似比。

从以上分析可知，要使模型与原型相似，一切对应的变量均须相似，而所有对应变量又都有表征其特征的值存在，因此，在取相似系数和条件时，应充分考虑选取变量的特征值。

2．相似三定理

相似理论的基础是相似三定理、其具体内容表述如下。

(1)相似第一定理 凡彼此相似的现象必定具有数值相同的同名相似准则，且相应的相似指标为1。相似第一定理亦称相似正定理，它为模型试验带来了很多的方便。

现以牛顿第二定律为例。在力学相似系统中，力F、质量m、长度L和时间T之间的关系在原型实物系统中为：

对于另一个与原型相似的模型的力学系统则为：

两个系统相似，则其相应的物理量的比例即相似系数C应为常数，于是有：

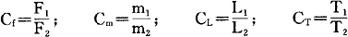
式(2)与式(3)相除，并以相应的相似系数代入经整理得：

于是

此式就称为力学系统的相似指标。它代表各物理量所采用的相似系数之间的关系。如若两系统相似，则相似指标为1。

从例示可知，相似系统中的相似系数的选取必须遵循相似指标为1的要求对此力学系统，表征F、m、L、T量的四个相似系数，其中三个可以任意选取，另一个必须由式(5)求得。

当再以式(4)代入式(5)中，可得各物理量之间的关系为：

该式所表示的这一无量纲组合被称为相似准则。它对所有的力学相似系统都是相同的。如将上述准则写成一般形式，并以π表示，则：

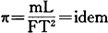
式中“idem”系拉丁文，其意表示同一数值。π亦非圆周率，是代表相似准则的专用符号。

(2)相似第二定理 一个物理系统具有n个物理量，其中k个物理量的量纲是相互独立的，则物理量可表达为(n－k)个相似准则π₁，π₂，…π_n－k的函数关系，即：

f(π₁，π₂，…π_n－k)=0 (7)

所以相似第二定理亦称π定理。

(n－k)个相似准则中，有些是由单值性条件(即给定条件)所决定，具有独立的已定相似准则：另一些则包含有待定物理量的待定相似准则。如果已定的和待定的相似准则关系是同一方程式中的自变量和因变量的关系，又两系统中相应已定相似准则相等，则相应待定相似准则亦随之相等。

当系统比较复杂，无法用一个相似准则说明问题时，就要用相似第二定理确定所需相似准则的数量。

例如图7．1．1－1所示悬臂梁，如何分析其系统弯曲强度相似时的参数关系。由材料力学可知，悬臂梁的弯曲应力公式为：

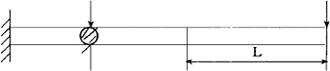
图7．1．1－1 悬臂梁

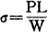
由式知该系统有四个物理量σ、P、L、W，按π定理n=4，其中力P及长度L是独立的基本量纲物理量，即k=2，则应力σ_。及抗弯切面系数W为导出物理量，因而应有n－k=2个独立相似准则。这样，除应力关系外，需再引入几何关系式，即：

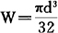
由两个关系式得到无量纲数群分别以π₁、π₂表达，即：

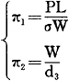
如若两个悬臂梁系统相似，由相似第一定理可知，

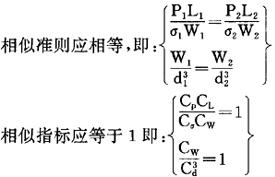
π定理表明，如果两个系统在物理上是相似的，它们的π值必定相等。在某些机械制造领域中，广泛采用模型试验作为产品开发和标准化的依据，其理论基础就是π定理。

(3)相似第三定理 对于同一类型的物理现象，如果单值条件彼此相等，且由单值条件的物理量所组成的相似准则在数值上相等，则这些现象必定相似。相似第三定理亦称相似逆定理。

单值条件是指用以与其他现象区别的条件，它包括：

几何条件，是以几何空间内的几何形状和大小所确定的条件。

物理条件，是以物理特性为依据所确定的条件。

边界条件，是以相邻环境为依据所确定的条件。

起始条件，是以起始状态为依据所确定的条件。

相似第三定理着重说明在模型试验时，必须满足系统的几何相似，物理参数相似、时间相似以及边界相似等等。对于较复杂的一些模型试验，其边界条件的模拟比较困难，在设计试验方案时应足够重视。采用有机模型试验时，温度对于应力和变形等均有明显的影响，应充分注意温度对试验精度的影响，并采取相应的措施。

以上就是相似三定理的基本内容。相似第一定理和相似第二定理只表明相似现象的性质。而相似第三定理则补充了判断相似所需的必要和充分的条件。

实际模型试验时，要使全部相似准则相等，往往是十分困难的，有时甚至是不可能的。这样就只能选择对物理现象起决定性作用的一、二个相似准则使之相等，其余准则可以不考虑，再用模型和原型的试验结果来判别模型的近似程度，这时称为近似模化，采用的是近似模型。