模糊评价

出处：按学科分类—工业技术 企业管理出版社《工程师手册》第285页（2049字）

在方案评价的过程中，有一部分评价目标如美观、安全性、舒适性、便于加工等无法定量分析，只能用好、差、受欢迎等“模糊概念”来评价。模糊评价就是利用模糊数学将模糊信息数值化，以进行定量评价的方法。

1．隶属度

模糊评价的表达形式不是分值的大，而是方案对某些模糊评价概念隶属度的高低。对于模糊概念一般不是简单的肯定(1)或否定(0)而是用0－1之间的一个实数去度量。某方案对“便于装配”的概念有八成符合，即称它对“便于装配”的隶属度是0．8。用函数表示不同条件下隶属度的变化规律称为“隶属函数”。隶属度可通过已知隶属函数或采用统计法求得。

(1)统计法求隶属度

如评价某种自行车，通过对一定数量顾客的调查，30%认为外观“很好”，55%评价为“好”，13%评价为“不太好”，2%认为“不好”，由此得到自行车外观对四种评价概念的隶属度分别是0．30、0．55、0．13和0．02。

(2)由隶属函数求隶属度

模糊数学的有关资料中推荐有十几种常用的隶属函数，可根据评价对象选择合适的隶属函数，从中求得特定条件下的隶属度。

2．模糊评价

(1)单评价目标的模糊评价

如对自行车外观的评价评价集(论域)X={X₁，X₂，X₃，X₄}={很好，好，不太好，不好}

对某种自行车的模糊评价集

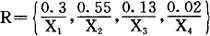
简写为R={0．3，0．55，0．13，0．02}

模糊评价集中的数值分别为各评价标准的隶属度。

(2)多评价目标的模糊评价

先求各评价目标及加权系数的模糊评价矩阵，根据模糊矩阵合成规律将矩阵合成即得某方案的综合模糊评价集。

评价目标集Y={y₁，y₂，……y_n}

评价集X={X₁，X₂，……X_。}

加权系数集A={a₁，a₂，……a_n}

某方案对几个评价目标的模糊评价矩阵

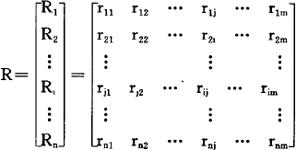
考虑加权的综合模糊评价

B=AR=[b₁ b₂…b_j…b_m]

模糊矩阵的合成有几种模型，在模糊评价中常用以下两种方法求bj。

①M(∨，∧)：按取小(∧)取大(∨)运算进行矩阵合成。“∧”、“∨”为Zadeh算子。

a∧b=min(a，b)

a∨b=max(a，b)

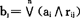
即b_j=(a₁∧r_1j)∨(a₂∧r_2j)∨…(a_n∧r_nj)而j=1，2，…，m

这种运算简洁明了，小中取大突出了权重和隶属度中主要因素的影响，但由于(∧，∨)运算会丢失部分信息，对评价目标较多，加权系数绝对值小的情况下，往往得不到合理的评判结果。

②)M(·，+)：按乘加运算进行矩阵合成

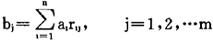
这种运算综合考虑了各项隶属度和权重的影响，在工程设计参数的模糊评价和模糊优化设计时效果较好。

3．方案比较

方案比较时考虑两个原则：

(1)最大隶属度原则。对每个方案按综合模糊评价中隶属度最高的一级定其级别。

(2)方案优劣排队时同级中隶属度高者为先。注意应以本级及更高级隶属度之和为准进行比较。