网络图的绘制和计算

出处：按学科分类—工业技术 企业管理出版社《工程师手册》第525页（6013字）

1．网络图的绘制方法

网络图是网络计划技术的基础。网络图的绘制方法，一般分为三个步骤：任务分解、作图和编号。

(1)任务分解

任务分解就是把一个工程或一项任务分解成若干道工序或作业，并确定各工序之间的关系。任务分解，最重要之点在于合理确定任务活动的开展顺序，以建立网络的逻辑基础。为了正确确定工程活动的开展顺序，搞好任务分解，必须了解工程活动的下列基本性质和特点。

①时间上的序进性和非序进性。，序进性是指活动的展开严格遵循工艺要求的顺序，在时间上先后进行，如先基础工程后主体结构，先零部件加工后总机装配等等。非序进性是指活动不受施工工艺要求的顺序展开，在时间顺序上无严格限定制约关系，如室内与室外工程间的安排等。序进性活动，组成了序进性工序，它属于串联或串联并联混合活动；非序进性活动则组成平行工序，属于并联活动，如图4．4．3－1所示。

a．序进性工序

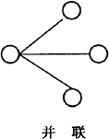
b．非序进性工序

图4．4．3－1

②)空间上的协调性。工程活动不仅要求在时间上协调，而且还要求在空间上协调。空间上协调包括平面上协调和立体上协调。平面作业有点型、线型、网型及其相互交叉；立体作业有地下、地面和架空三类；还有平面与立体交叉作业等等。

工程活动展开顺序，除了考虑上述要求外，还应注意季节性特点，零部件协作及配套工程保证条件等，以满足建设需要，提高经济效益，达到技术上可行，经济上合理。

工程任务展开以后，应按各工序的顺序编制作业明细表。

(2)作图

作图是按照作业明细表标明的各项作业的先后顺序，在相邻工序的结合处画上事件符号“〇”，然后用箭线连接起来，便可绘出网络图。网络图的作图方法如下。

①双代号法。双代号法是用一个箭线表示一个工序，工序名称写在箭线上部，工序作业时间写在箭线下部。箭尾表示工序的开始，箭头表示工序的结束，前后两相邻箭线的结合处画上事件符号圆圈“〇”。双代号法为国内外广泛应用的方法。

②网络图的绘制顺序。网络图是有向图，要从左至右排列，不能有缺口和回路。按工序的先后顺序画图：工序A完工后，工序B、工序C才能开工；A为B、C的紧前工序，B、C为A的紧后工序(其画法如图4．4．3－2所示)。

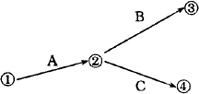
图4．4．3－2

③虚工序的画法。虚工序是指作业时间为零的虚任务，它不需要时间、资源和费用，只用来表示相邻工序之间的衔接关系。虚工序用虚线表示。如图4．4．3－3所示。

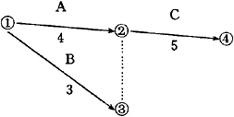
图4．4．3－3

④平行作业的画法。在实践中，为了加快工程进度，合理安排施工，有些工序可以同时并行，即采用平行作业方式，平行作业，在网络图中，一般画成并联形式，也可用虚工序表示。其画法如图4．4．3－4所示。

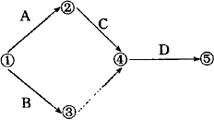
图4．4．3－4

⑤交叉作业画法，交叉作业是在一项复杂工程中，为缩短生产周期，加快工程进度而实行的平行作业与其他作业互相交叉进行的作业方式。在网络图中，交叉作业的画法如图4．4．3－5所示。

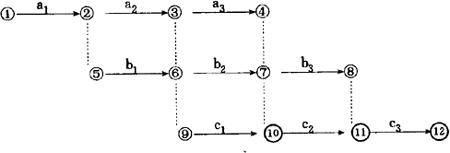
图4．4．3－5

⑥始点与终点的画法。一张网络图，只能有一个始点和一个终点，用以表示工程的开始和完成。但在实践中，有些工程需从几个工序同时开工，也有的需几个工序同时完工后才能完成。这种情况，在网络图上的画法如图4．4．3－6所示。

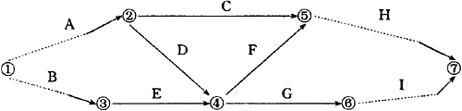
图4．4．3－6

(3)编号

编号是指按照作业明细表排列的顺序，对每个结点编上号码。编号一般采用前进法，即从始点起，从左至右编排，每个事件结点都应有一个顺序编号，号码不能重复使用。一个工作的两个相关事件可写成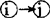，但应符合i＜j的要求。编号从始点开始，由小到大，终点顺序编号最大。同时，考虑到一项工作任务有可能细分成几个工作，编号时可在中间留有适当的余号，以备调整时填充。

2．网络图时间参数的计算与确定

网络图时间参数，包括作业时间、事件时间、线路时间、时差及关键线路等。其计算和确定的方法如下。

(1)作业时间的计算

作业时间(也称工序时间)，是指完成某一项作业所需要的延续时间，以T_E(i，j)表示。作业时间，一般是根据工时定额来确定。在没有工时定额的情况下，作业时间难于确切地确定，只能提出一些估计的数值。此时，根据概率和数理统计原理，常用三点估计法求出平均值，确定作业时间。其计算公式如下：

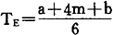
式中：T_E－平均作业时间；

a－最小的估计时间，或最乐观时间；

b－最大的估计时间，或最悲观时间；

m－a、b二者之间的估计时间，或最可能时间。

T_E实际上只是一个平均估计值，偏差是不可避免的。为了查明该估计值概率分布的离散程度，可计算完成该作业所需时间的方差值。计算公式如下：

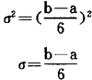
式中σ为均方差。由σ值可知平均估计值T_E的代表性。σ值愈大，表明T_E离散程度愈大，则其代表性愈小；反之，σ值愈小，则表明T_E的离散程度愈小，其代表性愈大。

(2)工序时间参数的计算

①工序最早开始时间，以T_ES(i，j)表示。就是箭尾事项的最早开始时间。即：

T_ES(i，j)=T_E (i)

工序最早开始时间，也可用其紧前工序的最早开始时间加上本工序时间来计算。如同时有几个紧前工序时，则选取其中最早开始时间与本工序时间之和为最大者。否则，在此之前，箭头事项不可能开始。计算公式如下：

T_ES(j，k)=max{T_Es(i，j)+T(i，j)} (j=2、3……n)

式中：T_ES——工序最早开始时间；

j、k——工序箭尾事项与箭头事项编号；

T(i，j)——工序作业时间。

②工序最迟开始时间，以T_LS(i，j)表示，是指工序在此时间最迟必须开始，否则会影响后续工序如期开工。其值等于箭头事项的最迟结束时间减去本工序的工序时间之差。计算公式为：

T_Ls(i，j)=T_L(j)－T(i，j)

亦可用紧后工序的最迟开始时间减去本工序时间求得。当紧后工序同时有几个时，可选取其中最迟开始时间与本工序时间之差为最小者。即：

T_Ls(i，j)=min{T_Ls(j，k)－T(i，j)}

③工序最早完成时间，以T_EF(i，j)表示。等于工序最早开始时间加上本工序作业时间之和，即：

T_EF(i，j)=T_Ls(i，j)+T(i，j)

④工序最迟完成时间，以T_LF(i，j)表示。等于工序最迟开始时间与工序作业时间之和，即：

T_LF(i，j)=T_Ls(i，j)+T(i，j)

(3)事项(事件)时间参数的计算

①事项最早开始时间，以T_E(i)表示。是指从始点起到本事项的最长路程的路长时间。在此时间之前，该事项不具备开工条件。事项最早开始时间，是从始点事项开始，自左向右逐个事项计算，直到本事项为止，始点事项的最早开始时间等于零，即T_E(1)=0。一个箭头事项的最早开始时间，等于它的箭尾事项的最早开始时间与箭杆上的时间(工序时间)之和。若同时有几支箭线与箭头事项相接，则选取其中箭尾事项最早时间与箭杆上时间之和为最大值者。计算公式如下：

T_E(j)=max〔T_E(i)+T(i，j)〕 (j=2、3……n)

式中：T_E(j)－箭头事项的最早开始时间；

T_E(j)－箭尾事项的最早开始时间；

T(i，j)－工序时间。

②事项最迟完成时间，以T_L(j)表示。是指在这一时间该事项必须完成，否则会影响紧后工序的按时开工。它的计算是从终点事项开始，自右向左，由后往前逐个事项倒算。直到始点事项为止。终点事项的最早开始时间就是该事项的最迟完成时间，即T_L(n)T_E(n)。一个箭尾事项的最迟完成时间，等于它的箭头事项的最迟完成时间减去箭杆上的时间之差。如从此箭尾事项同时发出几支箭线时，则选取其中箭头事项最迟完成时间与箭杆上时间之差为最小者。否则，过此时间，必将影响后续工序的按时开工。其计算公式如下：

T_L(j)=min〔T_L(j)－T(i，j)〕

式中：T_L(j)——箭尾事项最迟完成时间；

T_L(j)——箭头事项最迟完成时间；

T(i，j)——工序时间。

3．时差的计算与关键线路的确定

(1)时差的计算

时差是用来表明该项工作可以利用的机动时间。时差就是在不影响整个工程任务完工时间的条件下，某项工作从最早开始时间到最迟开始时间，中间可以推迟的最大延迟时间。时差也叫做“机动时间”、宽裕时间”或“缓冲时间”。时差有两种：即总时差和单时差。

总时差表明，在不影响总工期完成的条件下，该工作允许推迟的最大时间幅度，以TF(i，j)表示。其计算公式如下：

TF(i，j)=T_Ls(i，j)－T_Es(i，j)

或 TF(i，j)=T_LF(i，j)－T_EF(i，j)

=T_L(j)－T_E(i)－T(i，j)

式中：TF(i，j)——工作的总时差；

T_LS(i，j)——工作的最迟开始时间；

T_Es(i，j)——工作的最早开始时间；

T_LF(i，j)——工作的最迟结束时间；

T_EF——工作的最早结束时间；

T_L(j)——箭头事项的最迟完成时间；

T_E(i)——箭尾事项的最早开始时间；

T(i，j)——工序i－j的工作时间。

单时差是表明在不影响下一个工序的最早开工时间的前提下，该工序允许推迟的最大时间幅度，以FE(i，j)表示。其计算公式如下：

FF(i，j)=T_E(j)－T_E(i)－T(i，j)

=T_E(j)－T_EF(i，j)

=T_Es(j，k)－T_EF(i，j)

式中：T_ES(j，k)——紧后工序的最早开始时间。

单时差只能在本作业中使用，不能转移给其他工序使用。各个单时差之总和，应等于总时差的最大值。

时差表明了工序可以机动利用时间潜力。时差越大，说明机动时间越多，时间潜力也就越大。正确地计算和利用时差，是网络计划技术中的一个重要问题。它为计划进度的安排提供了可供选择的可能性，并且又是确定关键线路的主要依据。

(2)关键线路的确定

关键线路又称关键路线，它可以借助于时差来确定。在网络图中，总时差等于零的作业(工序)叫做关键作业(工序)，由这些关键作业(工序)连接起来的可行路线，就是关键路线。只要从始点事项起，沿着箭头方向至终点事项止，逐段找出总时差为零的工序，并把它们连接起来，便找到了关键线路。

确定关键线路是网络计划技术的核心。关键线路是影响整个工期的决定性环节。如果关键线路的工作进度延迟，则整个工期就要拖延。相反，如能采取措施加速关键线路的工作进度，则整个工期就可以提前。可见，掌握关键线路对组织和指挥生产是至关重要的。