一元线性回归预测法

出处：按学科分类—工业技术 企业管理出版社《工程师手册》第714页（1570字）

一元线性回归预测法适用于预测对象主要受一个相关变量影响且两者间呈线性关系的预测问题。一元线性回归的工作程序如下：

1．建立一元回归模型。设有一组反映预测对象与某变量之间因果关系的样本数据(可以是历史序列数据，也可以是历史截面数据)：

x₁x₂…x₁…x_n

y₁y₂…y_i…y_n

根据经验判断或观察分析(如通过作散点图观察)，两者之间确有较明显的线性相关关系，则可建立如下一元回归模型

y=a+bx

式中y——因变量(预测对象)；

x——自变量；

a、b——回归系数。

2．由已知样本数据根据最小二乘法原理求出回归系数。计算公式为：

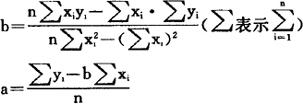
式中n——样本数据点数目，最好不少于20；

x_i、_yi——样本数据。

样本数据应经过分析筛选，去掉不可靠和明显不正常的数据点。

3．计算相关系数r，进行相关检验。

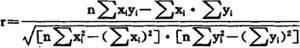
0≤|r|≤1，|r|愈接近1，说明x与y的相关性愈大，预测结果的可信程度愈高。一般可用计算出的相关系数r与相关系统临界值r_c相比较，r_c是由样本数n和显着性水平a两个参数决定的，实际工作中可由相关系数临界值表查出。a表示用线性方程在一定区间描述x与y的相关关系不可靠的概率。1－a称为置信度，表示在一定区间用线性方程描述x与y的关系令人置信的程度。只有当|r|＞r₀时，预测模型(回归方程)在统计范围内才具有显着性，用回归方程描述y和x的关系才有意义。

4．求置信区间。由于回归方程中自变量x与因变量y之间的关系并不是确定性的，所以对于任意的x=x0，我们无法确切地知道相应的y₀值，只能通过求置信区间判定在给定概率下y₀实际值的取值范围。在样本数为n，置信度为1－a的条件下，y_a的置信区间为：

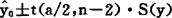
式中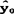——与x₀相对应的根据回归方程计算的y₀的估计值。

t(a／2，n－2)——自由度为n－2，置信度为1－a时t分布的临界值，可参考有关文献由t

分布表查出。

S(y)——经过修正的因变量y的标准差。

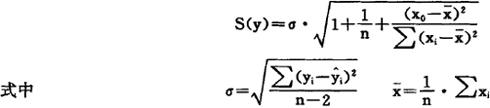
在实际的预测工作中，如果样本数足够大，上式中的根式近似地等于1。当置信度取1－a=0．95时，t(a／2，n－2)约等于2，y₀的置信区间近似为y₀±2σ，这意味着y₀的实际值发生在(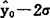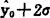，)区间内的概率为95%。当置信度取1－a=0．99时，t(a／2，n－2)约等于3，y₀的置信区间近似为。

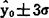5．分析情况做预测。回归方程是根据历史数据建立的，利用回归方程做预测的前提是确认预测对象与所选自变量的关系及影响预测对象的环境条件未来没有重大变化，因此必须对变量间的关系及环境因素的变化作认真的分析，必要时应对预测模型作适当的修正。在此基础上才可根据求得的回归方程进行预测。