移动平均法
出处:按学科分类—工业技术 企业管理出版社《工程师手册》第716页(2217字)
移动平均法是用分段逐点推移的平均方法对时间序列数据进行处理,找出预测对象的历史变动规律,并据此建立预测模型的一种时间序列预测方法。
用移动平均法平滑处理的具体作法是每次取一定数量的时间序列数据加以平均,按照时间序列由前向后递推,每推进一个单位时间,就舍去对应于最前面一个单位时间的数据,再进行平均,直至全部数据处理完毕,最后得到一个由移动平均值组成的新的时间序列。视需要这种移动平均处理过程可多次进行。
1.一次移动平均值的计算
设实际的预测对象时间序列数据为yt(t=1,2,…,m),一次移动平均值的计算公式为
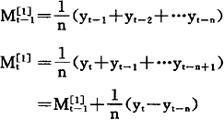
式中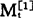 _—第t周期的一次移动平均值;
_—第t周期的一次移动平均值;
n——计算移动平均值所取的数据个数。
由上式可知,当n=1时,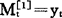 ,移动平均值序列就是原数据的实际序列;当n等于全部数据的个数m时,移动平均值即为全部数据的算术平均值。可以看出,n的大小对平滑效果影响很大,n取得小,平滑曲线灵敏度高,但抗随机干扰的性能差;n取得大,抗随机干扰的性能好,但灵敏度低,对新的变化趋势不敏感。所以n的选择是用好移动平均法的关键,针对具体的预测问题,选择n时,应考虑预测对象时间序列数据点的多少及预测限期的长短。通常n的取值范围可在3~20之间。
,移动平均值序列就是原数据的实际序列;当n等于全部数据的个数m时,移动平均值即为全部数据的算术平均值。可以看出,n的大小对平滑效果影响很大,n取得小,平滑曲线灵敏度高,但抗随机干扰的性能差;n取得大,抗随机干扰的性能好,但灵敏度低,对新的变化趋势不敏感。所以n的选择是用好移动平均法的关键,针对具体的预测问题,选择n时,应考虑预测对象时间序列数据点的多少及预测限期的长短。通常n的取值范围可在3~20之间。
通过一次移动平均处理,削弱了随机干扰的影响,较明显地反映出了预测对象的历史变化趋势。但应该注意到,当实际数据随时间推移发生变化时,一次移动平均值的变化总是落后于实际数据的变化,存在着滞后偏差,n取得越大,滞后偏差越大。
2.二次移动平均值的计算
二次移动平均值要在一次移动平均值序列的基础上计算,计算公式为:
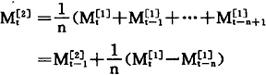
式中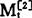 ——第t周期的二次移动平均值。
——第t周期的二次移动平均值。
二次移动平均值序列的线型比一次移动平均值序列的线型更加平滑,同时,二次移动平均值序列对一次移动平均值序列也有一个滞后偏差。
3.利用移动平均值序列作预测
如果实际的时间序列数据没有明显的周期变动,近期的移动平均值序列没有明显的增长或下降趋势,可以直接用最近一个周期的一次移动平均值,作为下一周期的预测值。也就是说,当最近一个周期为t时,可以认为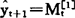 。如果实际的时间序列数据有明显的周期变动,近期的移动平均值序列有明显的增长或下降趋势,就不能直接用一次移动平均值作预测。这是因为,移动平均值的变化总是滞后于实际数据的变化,当预测对象有明显的增长趋势时,直接用一次移动平均值作预测会使预测值偏低,当预测对象有明显的下降趋势时,直接用一次移动平均值作预测会使预测值偏高。在这种情况下,如果预测对象的变化趋势呈线性,可以通过建立线性预测模型作预测。
。如果实际的时间序列数据有明显的周期变动,近期的移动平均值序列有明显的增长或下降趋势,就不能直接用一次移动平均值作预测。这是因为,移动平均值的变化总是滞后于实际数据的变化,当预测对象有明显的增长趋势时,直接用一次移动平均值作预测会使预测值偏低,当预测对象有明显的下降趋势时,直接用一次移动平均值作预测会使预测值偏高。在这种情况下,如果预测对象的变化趋势呈线性,可以通过建立线性预测模型作预测。
线性预测模型的一般形式为:
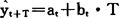
式中t——目前的周期序号;
T——由目前到预测周期的周期间隔数;
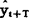 ——第t+T周期的预测值;
——第t+T周期的预测值;
at——线性预测模型的截距;
bt——线性预测模型的斜率,即每周期预测值的变化量。
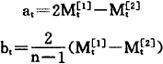
at与bt的计算利用了移动平均处理过程中存在滞后偏差这种现象。
当一次移动平均值序列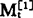 的近期数据呈线性增长或线性下降时,相应的
的近期数据呈线性增长或线性下降时,相应的 也应呈线性增长或线性下降,
也应呈线性增长或线性下降,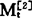 滞后于
滞后于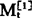 。由公式
。由公式
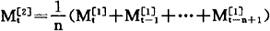
可知,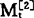 相对于
相对于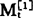 的滞后时间为:
的滞后时间为:
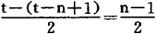
设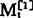 与
与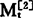 的单位时间增量均为bt,则
的单位时间增量均为bt,则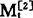 相对于
相对于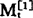 的滞后值为
的滞后值为
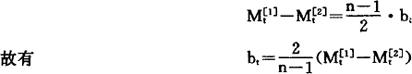
at为线性预测模型的截距,也就是预测趋势线的起始点。若用实际观察值yt作at,则受偶然性因素的影响较大,若用一次移动平均值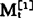 作at,又存在着滞后偏差。故设想:由于
作at,又存在着滞后偏差。故设想:由于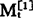 近期数据变动呈线性,根据预测模型得出的预测值
近期数据变动呈线性,根据预测模型得出的预测值 近期也有线性变动趋势。
近期也有线性变动趋势。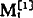 滞后于
滞后于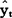 ,滞后时间为
,滞后时间为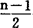 个周期,滞后值为
个周期,滞后值为
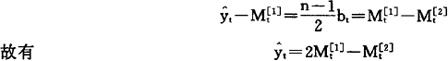
如果把第t周期作为预测方程的起始周期,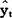 也就是方程的截距at,即
也就是方程的截距at,即