原子频标

出处：按学科分类—工业技术 企业管理出版社《计量专业工程师手册》第421页（5763字）

原子频标是利用原子跃迁产生标准频率的装置。分非自激型和自激型两种，通常称为被动型和主动型。

被动型原子频标中的原子谐振器相当一个鉴频器。其工作原理是石英晶振的输出信号经变换后，产生原子跃迁所需的激励信号，其频率在原子谐振器内与跃迁产生的频率进行比较，若存在频差，就相应产生一控制信号调整晶振的频率，使频差为零。这个过程由锁相环路完成。相位锁定后，晶振输出频率的准确度就等于原子跃迁频率的准确度。前边介绍的铯原子时间频率基准就是一种被动型原子频标。

主动型原子频标中的原子谐振器相当一个自激振荡器，其本身能自发产生高度准确的微波频率，然后通过锁相环路对一台晶振的频率进行锁定。

本节只介绍目前正在实用中的三种原子频标：铯束原子频标，铷气泡原子频标和氢脉泽原子频标，前两种属于被动型，后一种属于主动型。

原子谐振器是原子频标的核心部分。具有三种功能：跃迁原子的制备、跃迁的发生和跃迁信号的检测。用不同原子建立的频标，其谐振器的结构可能不同，但所完成的任务都是一样的。这里对谐振器的功能做为共性加以介绍。

1．跃迁原子的制备——选态

目前实用的原子频标与前边介绍的时频基准一样，都是利用原子在其基态的两个超精细能级间的跃迁。由于这两个能级靠的很近，在正常状态下，分布在这两个能级上的原子数几乎是相等的(见图8．2－4)。而跃迁的方式都是受激辐射，即在外界信号的感应下，低能级的原子跳到高能级上的同时，几乎同样数量的高能级上的原子也跳到了低能级上。于是跃迁前后每一能级上的原子总数几乎不变，原子的能量也几乎不变。这样，就无法判断跃迁是否发生了。

图8．2－4 原子在能级上的分布

为了检测到跃迁的信号，就得使跃迁前两个能级上的原子数发生大的变化，或者只选择某一能级上的原子，去掉另一能级上的原子。这种过程称为选态。目前在实用频标上使用的方法有两种，一是磁选态，二是光抽运选态。

(1)磁选态

如前所述，电子绕原子核旋转，相当一个闭合电流，从而使原子具有磁矩，称为轨道磁矩。此外，核本身及电子本身也都在自旋，也都产生自旋磁矩，自旋磁矩与轨道磁矩合成的结果，产生了原子的超精细能级。由于电子自旋具有两种完全相反的方向，于是在两个超精细能级上的原子的合成磁矩就可简单的看成方向相反。这种磁矩相反的原子经过一个很强的外磁场时，就会受到方向相反的力。从而偏向两种不同的方向，如图8．3－5所法

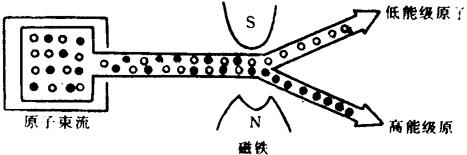
图8．3－5 磁选态

两个能级上的原子在空间被分开后，就可利用任一能级上的原子的跃迁。例如，若选用低能级上的原子，则跃迁前，高能级上的原子被分离掉了。适当配置检测器，就可检测到由低能级跃迁到高能级上的原子，而检测不到跃迁前原来高能级上的原子。

(2)光抽运选态

其原理是利用满足一定频率条件的光，把两个超精细能级中某一能级上的原子抽运到另一能级上。可用图8．3－6简单说明。

图8．3－6 光抽运选态

设E₁，E₂为原子基态的两个超精能级，外来光照射前，两能级上原子数几乎相等，假定均为4个。E₃为原子的激发态，是原子的不稳定状态，即原子在此能级上停留不住，假定原子数为零。此时状态如图(a)所示。现在外加一束光，其频率等于原子在E₁与E₃间跃迁时的辐射频率。在光照射时，E₁上的原子会吸收一部分能量跃迁到E₃上去，假定4个原子全部跳到E₃上，如图(b)所示。由于E₃是不稳定能级，原子到E₃后又会自发的跳回到基态去。又由于E₁与E₂相差很小，与E₃之差近似相等。故E₃上的原子会以相同的几率同时跃迁到E₁和E₂上，这样第一次抽运后，E₁上原来的原子就有一半落到了E₂上。如图(c)所示。如此循环下去，最后E₁上的原子几乎全部转移到了E₂上。于是可以利用E₂上的原子向E₁的跃迁产生标准频率。

铯原子频标和氢原子频标使用的是磁选态，铷原子频标使用的是光抽运选态。

2．跃迁的发生与检测

(1)被动型原子频标

在这种频标内，原子跃迁的发生需要具有一定功率和满足频率条件的激励信号。激励信号由电子线路产生，最后输入到原子谐振器内的微波谐振腔上，原子在微波腔产生的电磁场的作用下发生跃迁。跃迁信号的检测与选态类似，也有两种方法：磁检测如光检测。图8．3－7和图8．3－8分别给出了铯原子频标和铷原子频标的原子谐振器的主要构成部分。

图8．3－7 铯原子频标的谐振器

图8．3－8 铷原子频标的谐振器

铯原子频标的微波腔为U形腔，实际上是分两路的波导管。检测磁铁的形状和极性安置与选态磁铁完全一样。由加热铯炉喷出的气态铯原子束经过选态磁铁后，低能级上的原子向上偏转，高能级上的原子向下偏转并穿过微波腔。如果未加激励信号，穿过微波腔的原子不发生跃迁，到达检测磁铁后继续向下偏转，离化丝接收不到原子。反之，加入激励信号后，原子在微波场的作用下发生跃迁，变成高能级，穿过检测磁铁后向上偏转，打到离化丝上产生离子流，再经过电子倍增器变成较强的跃迁信号电流。

铷原子频标的微波腔为单一的园筒形，在腔内放置充有气体状的铷原子，光谱灯由Rb⁸⁷(铷原子的一种同位素)产生多频率的一束光，通过充有Rb⁸⁵(铷的另一种同位素)气体的滤光泡变成单一频率的抽运光，供微波腔内Rb⁸⁷原子跃迁前的选态用。未加激励信号时，在抽运光的作用下，微波腔内处于光通道上的原子很快就全部抽运到高能级上(见图8．3－6)，光就不会再被原子吸收，全部照射到光电管上，产生一个恒定的较强的光电流。当激励信号加入后，被抽运到高能级上的原子在微波场的作用下，将跃迁到低能级上。一旦低能级的原子出现，抽运光就会把它抽运到高能级上，从而使照到光电管上的光强减弱，光电流减小，减弱的部分就对应着跃迁电流的大小。

(2)主动型原子频标

主动型原子频标不需要外加激励信号，但仍需要一个微波腔，腔的谐振频率与被动型的微波腔一样，等于原子跃迁对应的频率。图8．3－9为主动型氢原子频标的原子谐振器的构成图。

图8．3－9 氢原子频标的原子谐振器

氢原子频标也是用磁选态，但采用六极磁铁。氢原子束经过选态磁铁后，高能级的原子被聚焦到中心线上，其他能级原子被散射掉。微波腔与铷原子频标一样也为园筒形，在微波腔内也有一个玻璃泡，但泡内并未予先充有氢气。只是接收选态后的氢原子，原子在泡内多次与壁碰撞后又由进入口逸出。即进入的原子在泡内存贮一段时间，故该泡称为存贮泡。

存贮泡内原子的跃迁也是受激辐射，但不是在外加激励信号的感应下，而是在微波腔内固有噪声的感应下发生的。类似于晶体振荡器的起振。噪声频谱是无限宽的，当某一部分噪声分量的频率等于氢原子在其超精能级间的跃迁频率时，存贮泡内的原子就会跃迁到低能级上，并放出一部分能量。这部分能量又会在微波腔上激起较强的振荡，又反过来进一步感应原子的跃迁，如此循环下去，最后在微波腔上就建立起一个稳定的、足够强的、其频率等于原子跃迁频率的微波信号，通过金属耦合环传给外界使用。这种跃迁信号的检测称为微波检测。

主动型原子频标是直接提供微波振荡信号，故又称为激射器，或直接用其英文名称的译音－脉泽。由于是直接提供振荡信号，故与被动型频标相比，其信号的频谱纯度高，频率短期稳定度好。

3．标准频率的获得——锁相环路

原子跃迁频率都很高，且数值也比较特殊，例如：铯原子频标的跃迁频为9192631770Hz，铷原子频标为6834682608Hz，氢脉泽为1420405752Hz。这些频率值都不利于广泛的直接使用。故实用的原子频标都是以其原子的跃迁频率为参考，通过锁相环路去控制一台5MHz的石英晶体振荡器。

被动型原子频标的锁相环路如图8．3－10所示

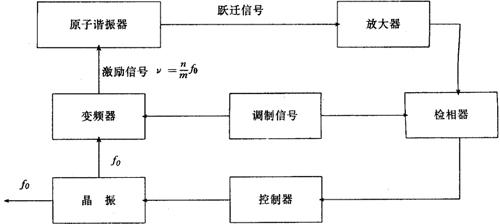
图8．3－10 被动型原子频标的锁相环路

f₀为晶振的频率，经过变频后变成，与原子的跃迁频率进行比较。当两者一致时与跃迁对应的检测信号达到最大(磁检测)或最小(光检测)。如图8．3－11所示。

图8．3－11 跃迁信号与激励频率的关系

当v≠v₀时，应产生一控制信号去调整晶振频率，最后达到v=v₀为止。这就要求在v＞v₀和v＜v₀时，控制信号应具有不同的极性。如果控制信号只简单的从图8．3－11的跃迁信号上获得则不能满足此要求。因为当v向不同方向偏离v₀时，跃迁信号都同样的减小或增加。而无极性变化。达不到向不同方向调整晶振频率的目的。为解决这一难题，在激励信号加上一个低频调制信号。调相或调频，这样所检测到的跃迁信号在图8．3－11所示的基础上也叠加上一个低频交流分量，如图8．3－12所示。

图8．3－12 加调制后的跃迁信号

从图示中可直观的看出，当激励信号的频率向不同方向偏离跃迁频率时，跃迁信号中叠加的交流成分具有相反的相位，此交流成分在检相器中与低频调制信号进行相位比较，从而产生极性不同的直流电压去控制晶振的频率。当v=v₀时，跃迁信号中的仍有交流成分，但其频率为调制信号频率的二倍，即二次谐波。当二次谐波与原来调制信号的基波进行检相时，检相器的输出电压为零。不去调整晶振频率。此时，锁相环路进入了稳定的锁定状态。晶振频率就与原子跃迁频率具有相同的准确度，可作标准使用。

主动型原子频标的锁相环路如图8．3－13所示。

图8．3－13 主动型原子频标的锁相环路

由于主动型原子频标的原子谐振器是一个自激振荡器，直接给出频率为v₀的振荡信号，故不用像被动型那样加调制信号，直接用此振荡信号为参考去锁定一台晶振。这是典型的无线电技术中的锁相环路。图中用了两次混频，把原子振荡信号变成较低的频率(F₂)后再与相应的由晶振产生的同值频率f₃进行检相，是由电路技术的易于实现和可靠等方面考虑的。

与被动型一样，环路稳定锁定后，晶振频就与原子跃迁频率具有相同的准确度，可作标准使用。

【参考文献】：

［1］王义遒等，量子频标原理，科学出版社，1986。

［2］吴守贤等，时间与频率，科学出版社，1983。

［3］黄秉英等，时间频率的精确测量，计量出版社，1986。

［4］王江现代测量技术，计量出版社，1987。

［5］P. Kartaschoff ,Frequency and Time,Academic Press ,1978.

［6］J. A. Barnes et al. ,Characterization of frequency stability, IEEE Trans Instrum Meas. IM —20,p.105—120,1971.

［7］Time and frequency:Theory and Fundamentals,NBS Manograph 140,1974.

［8］D. W. Allan ,The measurement of fruquency and frequency stability of precision oscillator,Proc.6th Ann PTTI Planning Meeting.

［9］Annual Report of the BIPM Time Sectina,1974.