曲面构件的计算展开
出处：按学科分类—工业技术 河南科学技术出版社《钣金技术手册》第448页（6132字）
(一)柱面的计算展开
柱面的计算展开是用解析计算代替平行线法，推导出柱面上结合线的展开曲线方程式或计算出展开曲线上若干点的坐标，得出点的运动轨迹，从而求得柱面的展开图。
1．平面斜截柱面构件
图6－51a为球磨机收尘落料筒的主视图和俯视图，图上标有已知的设计尺寸D、H和h(或α)，且h=D／2。作料筒展开图的关键是求出平面和筒体结合线的展开曲线上各点的坐标值，展开曲线上每个点P0将对应一个固定的角ψ0，故可根据两视图和展开图各尺寸间的几何关系，利用直角坐标系，推导出点P0的坐标：
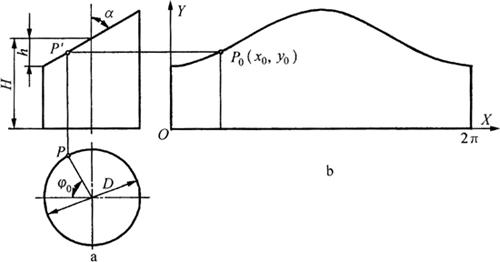
图6－51 收尘落料筒的计算展开
a．视图 b．展开图
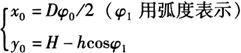
若ψ0用角度表示，角度α代表高度h时，点P0的坐标为
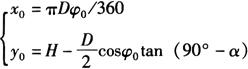
将上述两方程组中的ψ0消去，可得出结合线展开曲线的方程
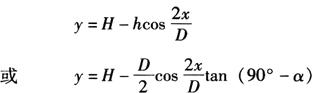
若将圆柱形料筒的圆周分为十二等份，每隔30°取一个ψ0的值代入上述曲线方程，则可计算出十二个点P的坐标值，即可画出落料筒的展开图(图6－51b)。
2．弧面斜截柱面构件
图6－52a为排烟进口筒的主视图和计算原理图。构件的已知尺寸是D、R、H和L。由于构件是由圆弧面斜截正圆柱形筒体，弧面和筒体结合线的展开曲线上的点P0将对应一个角ψ0，由各尺寸间的几何关系和角ψ0推导出点P0的坐标：
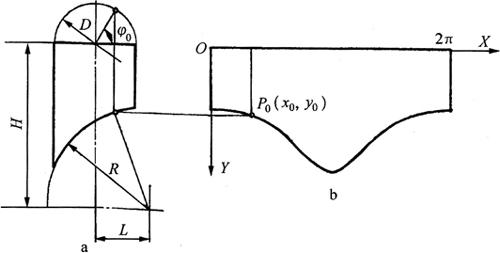
图6－52 弧面斜截排烟筒的计算展开
a．视图 b．展开图
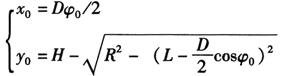
将上述方程组中的ψ0消去，可得出结合线展开曲线的方程
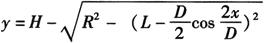
当圆弧的中心在圆筒的轴线上(即L=0)时，将y0和y方程式均可简化为
若将正圆柱形烟筒下端弧面圆周分为十二等份，每隔30°取一个ψ0值代入上述曲线方程，则可计算出12个点P的坐标，从而画出排烟筒的展开图(图6－52b)。
3．柱面直交柱面构件
图6－53a为异径直交三通管两视图，构件展开的已知尺寸是主管内半径R2、外半径R1、水平中心线至支管端面距离H；支管外半径r1、直交量f、中径D2和圆周各等分点与同一纵向直径夹角βn。构件展开的关键必须计算孔实形和支管展开尺寸，可采用上述结合线展开曲线方程计算如下：
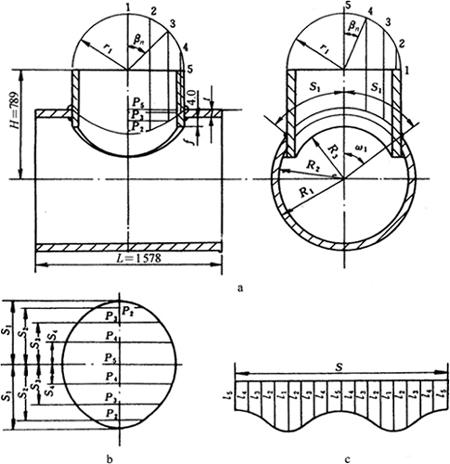
图6－53 异径直交三通管计算展开
a．主、侧视图 b．孔实形图 c．支管展开图
(1)支管展开尺寸的计算：
1)下端口半径：
R3=R2－f=501－40=461(mm)
2)各条等线长：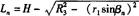 
代入已知尺寸得
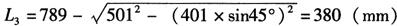
3)支管展开长(图6－51b)：
S=πD2=π×811=2548(mm)
(2)主管孔实形尺寸的计算：
1)主管孔各点与同一直径夹角：
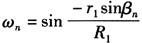
其中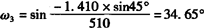 
。
2)主管纵向直径至各分点弧长：
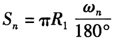
其中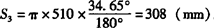 
。
3)孔实形横向距离：(图6－51b)
Pn=r1sinβn
其中 P3=410×sin45°=290(mm)。
4．柱面斜交柱面构件
图6－54a、b为等径斜交三通管的立体图和施工图，图5－54b、c中已知尺寸为主管长L1和L2、主管水平中心线至支管端面水平中心距离、主管内半径R2和外半径R1、支管外半径r1和中径D2、倾斜角α，以及圆周各等分点与同一直径夹角βn。构件计算展开方法如下：
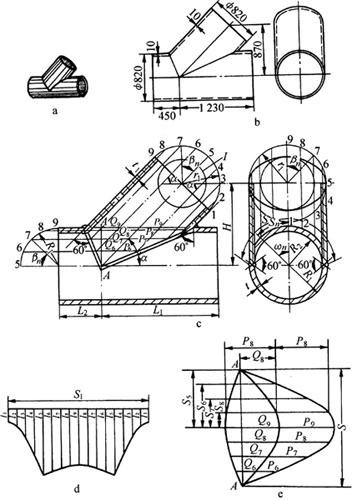
图6－54 等径斜交三通管的计算展开(单位：mm)
a．立体图 b．施工图 c．计算原理图 d．支管展开图 e．孔实形图
(1)支管展开尺寸计算：
1)支管任意素线：
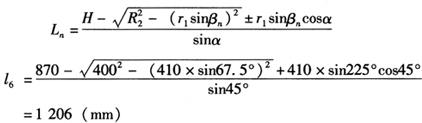
Ln式中 “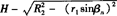
”见侧视图，“r1sinβncosα”见主视图。
2)支管展开长(图6－53d)：
S1=πD2=π×810=2545(mm)
(2)孔实形尺寸计算(图6－53e)：
S=πR1=π×410=1288(mm)
1)主管孔各点所对应圆心角：
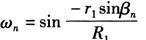
其中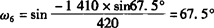 
。
2)主管孔各点所对应弧长：
其中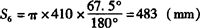 
。
(3)孔实形各素线长计算：
1)支管中心线左右素线相等(图6－53c中Ⅰ局部视图)。
2)中断面A－A至角度线：
Qn=R1sinβntanα
其中 Q6=410×sin22．5°×tan45°=157(mm)。
3)孔实形半长素线：
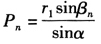
其中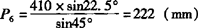 
。
(4)孔实形画法：以A－A正断面为基准线，以中点向上下量取S8、S7……各长得各点，以各点向右量取各Q长得各点，以各点为中点，各Pn长为长度横向量取得各点，圆滑连接各点即得孔实形图。
(二)锥面构件的计算展开
锥面的计算展开是用解析计算代替放射线法，推导出锥面上结合线的展开曲线的方程式，或计算出展开曲线上若干点的坐标，从而获得锥面的展开图。
1．平面斜截正圆锥面构件
图6－55a为平面斜截正圆锥管的主视图和锥底断面图，构件展开的已知尺寸是D、H、h和α，其平面与正圆锥面结合线的展开曲线上的每个点P0，将对应一个角ψ。，故可根据两视图和展开图各尺寸间的几何关系和ψ。角，利用极坐标系推导出点P0的坐标。在推导过程中，可先求出极坐标中θ0值，再利用相似三角形各边比例关系，求出P0点的坐标值。
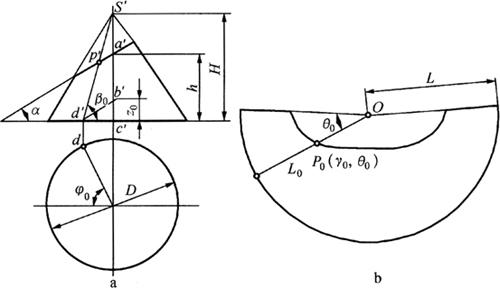
图6－55 平面斜截正圆锥面的计算展开
a．视图 b．展开图
由极坐标可直接得：
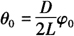
式中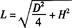 
。
在主视图中，过点d′作直线d′b′平行于直线p′a′，和中心线相交于b′，则b′c′间的长
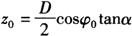
根据主视图上△s′d′c′与△b′d′c′两相似三角形中各线段的对应等比关系，可得
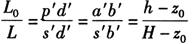
将z0式代入上式并整理，得
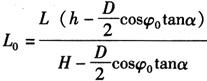
结果可得到P0点的坐标
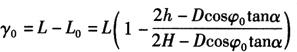
当α=0时，构件变为圆锥台，P0点的坐标
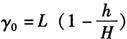
若将正圆锥管上端斜面圆周分为十二等份，各等分点至锥底的距离h、锥顶至锥底的距离H、锥底的直径D，以及沿斜面圆周每隔30°取一个ψ0值等代入上述γ0式中，即可计算出12个点P的坐标，从而画出展开图(图6－55b)。
2．弧面截正圆锥面构件
图6－56a为弧面截正圆锥管的主视图和计算原理图，构件的已知尺寸是R、r、H和H1。对展开图建立极坐标系，则可根据各尺寸间的几何关系和角ψ0推导出点P0的坐标。
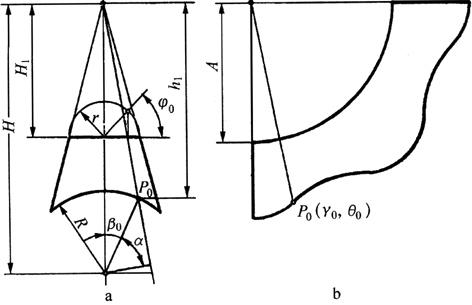
图6－56 弧面截正圆锥管的计算展开
a．视图 b．展开图
设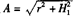
，，则
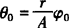，并从主视图中得出h0=H－Rcosβ0，且代入比例式
，经整理后得
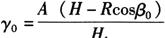
式中 β0=ω0－α0，则
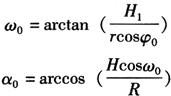
将ω0、α0求得值代入β0式求出β0，进而再代入γ0式即可求出P0点的坐标，从而求得展开曲线上若干点P的坐标，依此作出弧面截正圆锥面的展开图(图6－56b)。
3．柱面斜交正圆锥面构件
图6－57为柱面斜交正圆锥面构成的漏斗主视图和计算原理图，图中沿圆柱管与圆锥管结合线所在的平面将两管分开，可按前述“平面斜截柱面”和“平面斜截锥面”推导出的有关公式分别对两管进行计算展开。具体求法如下：
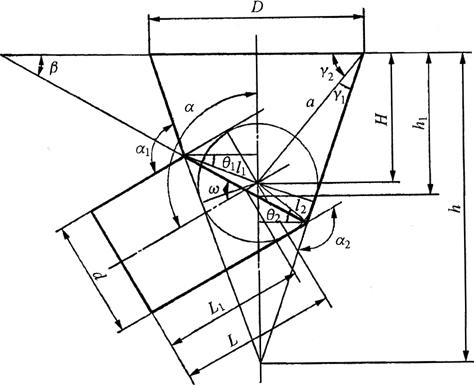
图6－57 柱面斜交圆锥管漏斗的计算原理
(1)有关参数的计算：即L1、ω和h、h1、β参数的计算。
式中 
；
。
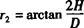又有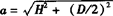 
；
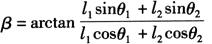
式中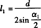 
；
；
；
；
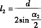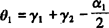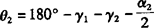α1=α－(90°－γ1－γ2)；
α2=α+(90°－γ1－γ2)；
ω=α－90°+β。
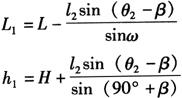
(2)圆柱管的计算展开：图6－58为圆柱管的视图和展开图，其展开曲线上P0点的坐标是：
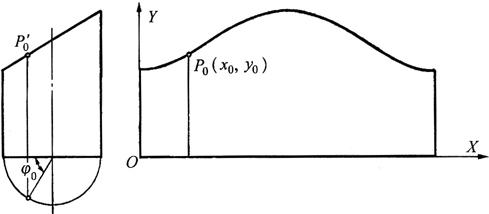
图6－58 圆柱管的计算展开
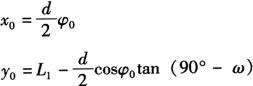
将圆柱管断面圆周十二等分点间隔30°取一个ψ0值代入曲线方程y0式，则可计算出12个点P的坐标，画出圆柱管的展开图。
(3)圆锥管的计算展开：图6－59为圆锥管的视图和展开图，其展开曲线上P0点的坐标是：
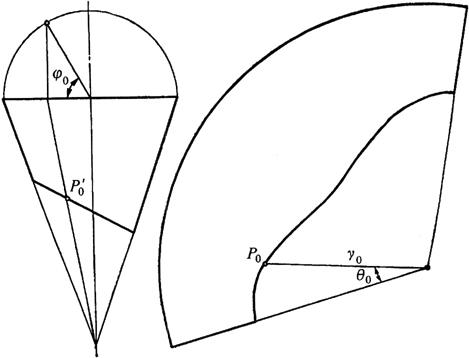
图6－59 图锥管的计算展开
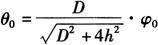
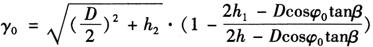
将圆锥管断面圆周十二等分点间隔30°取一个ψ0值代入上述曲线方程γ0式中，即可计算出12个点P的坐标，继而画出展开图。
(三)圆柱螺旋面构件的计算展开
图5－43和图6－45所示的圆柱正螺旋面，一个导程的近似展开图为一环形，若已知R、r和α时，则该环形即可画出。因此，可根据圆柱正螺旋面导程S、螺旋面的内径d和外径D，逐步计算如下：
(1)机叶外螺旋线展开长度：
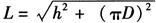
(2)机叶内螺旋线展开长度：
(3)机叶面宽(即环形宽度)：
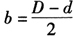
(4)环形内、外半径：由图5－43b可知，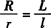
，R=r+b，若展开图圆环的内、外径以r、R表示，则得
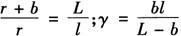
(5)展开图切去的圆心角：按圆心角公式可求得
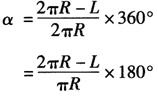
(6)圆心角所对的弦长：
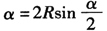
根据D、d、s计算出R、r、L、l、α、α之后，即可画出圆柱正螺旋面的近似展开图。在实际制作时，不必剪出α角。即在剪缝处直接绕卷成螺旋面，既可节省材料，又使各圈焊缝错位且均匀分布。