基本确定年金
出处：按学科分类—经济 中国商业出版社《金融企业会计制度实施手册上》第378页（2307字）
(一)利率与贴现率
期初投入的一笔资金在单位时间(如1年)所生利息与本金之比，称为实际利率，通常简称利率，以i表示。
期末投入的一笔资金在单位时间(如1年)所生利息与本金之比，称为实际贴现率，通常简称贴现率，以d表示。
贷款1：甲向银行借入100元钱，期限1年，利率6%。意味着银行立即付给甲100元；而在1年末甲还给银行100元本金并支付6元利息，合计106元，即终值为106元。
贷款2：甲向银行借入100元钱，期限1年，贴现率6%。意味着银行立即付给甲94元，即扣除6元利息后的100元；而在1年末甲还给银行100元，即终值为100元。
若以某个利率和某个贴现率投入相同的本金在相同的时间产生了相同的终值，则称该利率与该贴现率相等。设利率为i，贴现率为d，终值为1元，时间为一个单位(如1年)。则由贴现的含义(见贷款2)，得本金为(1－d)元。根据利率与贴现率相等的概念得，(1－d)元的本利和为1元，即，
(1－d)(1+i)=1 (3－2－1)
则
(1+i)－d(1+i)=1
d(1+i)=i
由
(1－d)(1+i)=1
还可得
(1－d)+i(1－d)=1
i(1－d)=d
v称为贴现因子，则
由
(1－d)(1+i)=1
还可得
1+i－d－id=1
i－d=id (3－2－7)
上述七个关于利率和贴现率的公式在年金的推导和计算中会经常用到。
(二)年金
一定时期内以固定的时间周期进行的一系列支付称为确定年金，简称年金。如每年初支付一次的年金，每季末支付一次的年金，每月初支付一次的年金等等。若每次地支付金额相同则称为定额年金。每年周期末支付的年金称为期末付年金，每个周期初支付的年金称为期初付年金。
1．期末付年金
为简化数学模型，假设每期末支付1元，在一定计量时期内共有n个支付周期，这样的期末付年金在计量时期末(n时点)和本利和，称为期末付年金的终值，记作
期末付年金如图3－2－1所示。
图3－2－1 期末付年金
第n期末支付的1元在n时点的本利和为1元，第(n－1)期末支付的1元在n时点的本利和为(1+i)元(其中i表示利率)，第(n－2)期末支付的1元在n时点的本利和为(1+i)2元，依此类推，第1期末支付的1元在n时点的本利和为(1+i)n－1元。所以，期末付年金的终值为，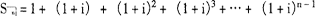
由等比级数求和公式得，
类似地，每期末支付1元、共支付n个周期的期末付年金在计量时期初(0时点)的贴现值，称为期末付年金的现值，记为
。如图3－1所示。第1期末支付的1元在0时点的贴现值为v=1／(1+i)元，第2期末支付的1元在0时点的贴现值为v2元，第3期末未付的1元在0时点的贴现值为v3元，依此类推，第n期末支付的1元在0时点的贴现值为vn元。显然，期末付年金的现值为，
可见，
2．期初付年金
每期初支付1元、共支付n期的年金在计量期末(n时点)的本利和称为期初付年金的终值，记为
。期初付年金如图3－2－2所示。
图3－2－2 期末付年金
类似于期末付年金终值公式的推导，将每个支付额在n时点的本利和相加，得期初付年金的终值为，
等比数列求和得，
其中，d=i／(1+i)=1－v=iv，是贴现率。
同理，每期初支付1元、共支付n期的年金在计量期初(0时点)的贴现值称为期初付年金的现值，记为
，如图3－2－2。期初付年金的现值为，
显然，
