齿轮连杆机构

出处：按学科分类—工业技术 北京出版社《现代综合机械设计手册中》第2007页（2070字）

齿轮连杆机构是齿轮机构和连杆机构的组合。由于连杆机构有多种形式，因此齿轮连杆机构的结构形式极为多样。但概括起来，可分为两类。一类的基础机构是自由度为2的差动轮系，通过自由度为1的四杆机构将其封闭起来，得到自由度为1的机构，如图5．8-4所示；另一类采用自由度为2的五杆机构作为基础机构，用自由度为1的齿轮机构将其封闭起来，如图5．8-5所示。

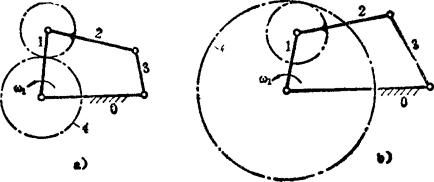
图5．8-4 用四杆机构封闭

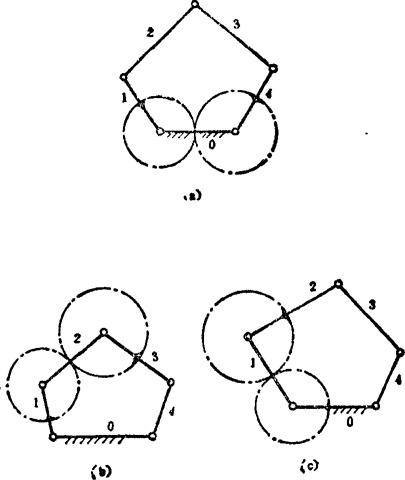
图5．8-5 用齿轮机构封闭

齿轮连杆机构从动件的运动，可以是匀速或非匀速运动，还可以具有瞬时停歇或部分逆转；齿轮连杆机构某些构件的点所描绘的轨迹曲线为高阶曲线，其形状比通常的连杆曲线丰富、多变。

图5．8-6所示齿轮连杆机构，由自由度为2的五杆机构和一对安装在机架的齿轮组合构成。两齿轮分别和连杆机构的杆1和杆4固结。机构运动时，连杆2和连杆3的铰接点描绘出复杂的运动轨迹。改变杆1和杆4的相对相位角、齿轮的传动比以及五杆机构各杆件的相对尺寸，可以得到不同的运动轨迹。如将一对相啮合的齿轮安置在铰链四杆机构的可动构件上，便构成图5．8-7所示的齿轮连杆机构。运动时，从动轮5上的M点将走出轨迹mm，其形状取决于连杆机构各构件的相对尺寸、齿轮传动比和M点在从动轮5上的位置。显然，M点的轨迹比单一的铰链四杆机构的连杆曲线更为复杂多样，因而容易实现预定的轨迹。

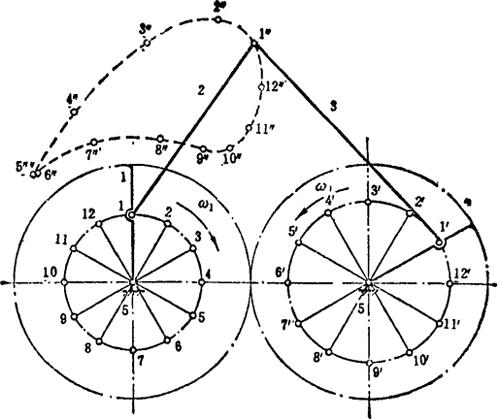
图5．8-6 齿轮连杆机构之一

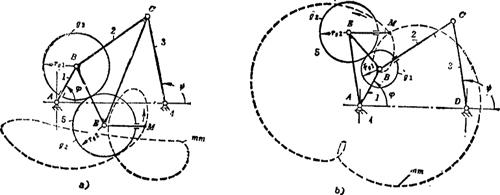
图5．8-7 齿轮连杆机构之二

图5．8-8所示齿轮连杆机构由差动轮系和连杆机构组合而成。曲柄2是差动轮系的系杆，行星轮和连杆3相固结，运动由曲柄输入，从空套在轴上的齿轮5输出。由差动轮系传动比公式可得

图5．8-8 齿轮连杆机构之三

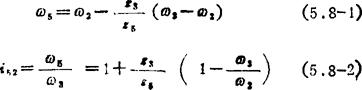
式中比值ω₃／ω₂可由四杆机构用解析法求出，得

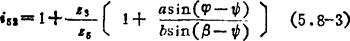
由上式可看出，改变连杆机构的参数或改变齿轮的齿数，都可使机构传动比i₅₂得到改变，因而可使从动轮实现复杂的运动规律，能短时停歇、短时反向转动。

图5．8-9所示为三齿轮式齿轮连杆机构。齿轮1与曲柄a固结，齿轮6空套于轴D上。由周转轮系传动比公式可得

图5．8-9 三齿轮式齿轮连杆机构

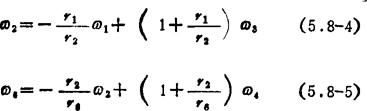
将(5．8-4)式代入(5．8-5)式可得

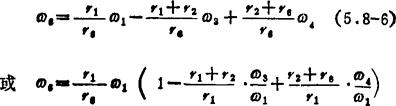
式中ω₃／ω₁和ω₄／ω₁可由四杆机构用解析法求出

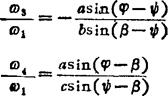
因 b=r₁+r₂、c=r₂+r₆，令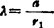，得

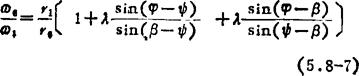
由式(5．8-7)可知：ω₀／ω₁的比值决定于r₁、r₆、φ、β、ψ和λ，并随φ的变化而变化，如图5．8-10所示，其变化规律近似正弦曲线型。λ对ω₆／ω₁比值的变化规律有明显影响当λ较小时(λ＜0．75)，输出轴作单向变速转动；λ增大后，输出轴会出现片刻停歇现象；λ再增大，输出轴将在一段区间内产生逆转运动。

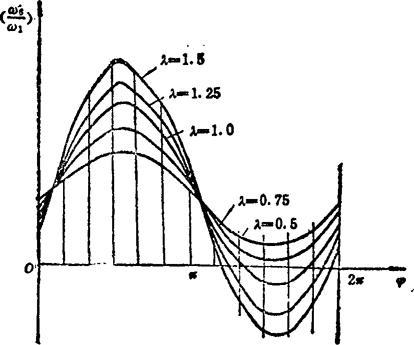
图5．8-10 ω₆／ω₁的变化规律

图5．8-11为另一种形式的行星齿轮连杆机构，由内啮合行星轮系和曲柄滑块机构组成。连杆3和行星轮2铰接于M点，齿数比z₀／z₂=3．机构运动时，行星轮2节圆上的M点将画出三支内摆线。适当选定连杆3的长度l，使以C为中心、l为半径的圆弧通过内摆线的M、M＇、M＂点，则当主动杆1由位置AL转过2φ角至位置AB＇时，从动滑块4将处于近似停歇状态(从动滑块的行程s=4r₂)。若把滑块4换成摇杆，则摇杆摇动时具有单侧停歇。

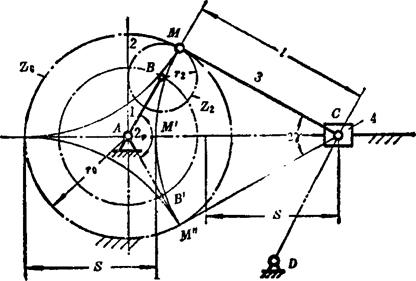
图5．8-11 行星齿轮连杆机构

以上行星轮式齿轮连杆机构运转时具有单侧停歇，是利用行星轮M点走出的内摆线近似于圆弧。若取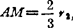，z₀／z₂=4，则M点走出具有近似圆角的正方形。把杆3铰接于M点，构成的齿轮连机杆构则具有双侧停歇，如图5．8-12所示(从动滑块的行程)。

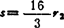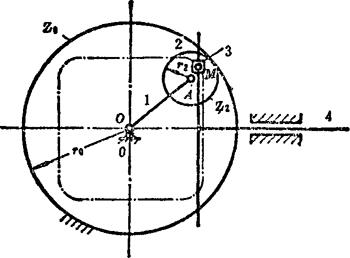
图5．8-12 具有双侧停歇的齿轮连杆机构