连杆曲线的性质

出处：按学科分类—工业技术 北京出版社《现代综合机械设计手册中》第2110页（1203字）

连杆曲线为六阶曲线，一般情况下与圆应有十二个交点，但其中有六个是无限远交点。铰链四杆机构的连杆曲线有三个位于有限远处的二重点C＇、C＂、C＂，它们都在焦点圆上，如图5．15-14所示。焦点圆是三角形A₀B₀M₀的外接圆，点A₀、B₀、M₀称为连杆曲线的焦点。而三角形A₀B₀M₀是连杆三角形ABC的同向相似三角形。三个有限远的二重点中，总有一个实点，另外两个可能为实点，也可能是虚点。

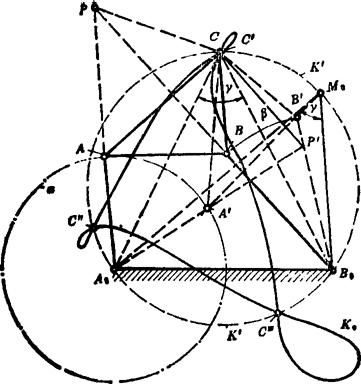
图5．15-14 有三个二重点的连杆曲线

如图5．15-15所示四杆机构A₀ABB₀，若把连杆平面上的C点选在瞬心P，这时C点成为连杆曲线的尖点。因为∠A₀CB₀=∠ACB=γ。所以，C点位于通过焦点A₀、B₀、M₀的焦点圆k＇上。

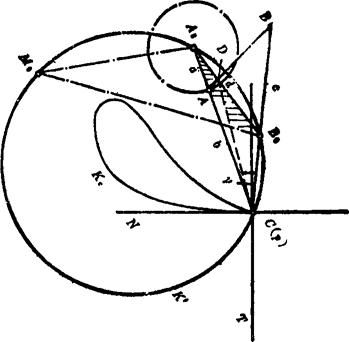
图5．15-15 有一个尖点的连杆曲线

尖点是特殊情况下的二重点。一般二重点为交叉点，有两个机构位置与其对应(参见图5．15-14，有连杆的两个位置AB和A＇B＇和二重点C＇相对应)，而尖点是折返点，只对应于一个机构位置，在机构综合中，连杆曲线上的尖点可用于产生瞬时停歇。如需使运动的始末都有停歇，则连杆曲线上应该有两个尖点，如图5．15-16所示C₁、C₂两个尖点。在图中由于A₁B₁=A₂B₂，B₁B₀=B₂B₀，∠A₁B₁B₀=∠A₂B₂B₀。所以，。由此可知，A₁B₀=A₂B₀。即对应于连杆两相邻位置A₁B₁C₁、A₂B₂C₂的极点P₁₂和铰链B₀相重合。由图可以看出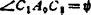，∠A₁A₀A_；=φ=180°-ψ，因此∠A₀A₁B₀=∠A₀A₂B₀=90°。即曲柄销A₁、A₂位于以机架A₀B₀=d为直径的圆k_d上。对于尺寸已知的四杆机构，如需确定连杆曲线上的两个尖点，只要以机架上的铰链中心A₀B₀为直径作圆k_d，它与曲柄圆的两个交点即为A₁、A₂，再画出对应的摇杆销B₁、B₂，最后作A₀A₁与B₀B₁的交点即尖点C₁，作A₀A₂与B₀B₂的交点即尖点C2。

图5．15-16 有二个尖点的连杆曲线

对称的铰链四杆机构，可以产生对称的连杆曲线。因为对称连杆曲线可使计算简化，故被优先用于传动机构和导引机构。

对称四杆机构上不同的连杆点画出不同的对称连杆曲线，不同的对称四杆机构上的连杆点也画出不同的连杆曲线。如图5．15-17所示，对心曲柄导杆机构和对心曲柄滑块机构上连杆点C所画出的对称连杆曲线是不同的。

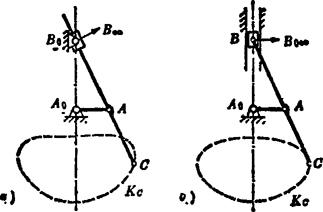
图5．15-17 对称连杆曲线