平面向量的坐标运算

出处：按学科分类—文体、科学、教育 商务印书馆国际有限公司《高中数理化公式定理大全》第50页（3183字）

1．平面向量的坐标表示

在平面直角坐标系内，分别取与x轴、y轴正方向相同的两个单位向量i、j作为基底，对任一向量a，有且只有一对实数x、y，使得a=xi+yj，则实数对(x，y)叫做向量a的直角坐标，记作a=(x，y)，其中x，y分别叫做a在x轴、y轴上的坐标，a=(x，y)叫做向量a的坐标表示．

相等的向量其坐标相同，坐标相同的向量是相等的向量．

2．平面向量的坐标运算

(1)若a=(x₁，y₁)，b=(x₂，y₂)，

则a±b=(x₁±x₂，y₁±y₂)．

(2)如果A(x₁，y₁)，B(x₂，y₂)，

则．

(3)若a=(x，y)，则λa=(λx，λy)．

(4)如果a=(x₁，y₁)，b=(x₂，y₂)，则a∥b充要条件是x₁y₂—x₂y₁=0．

(5)若a=(x₁，y₁)，b=(x₂，y₂)，

则a·b=x₁x₂+y₁y₂．

(6)若a=(x，y)，

则|a|²=a·a=x²+y²，|a|=．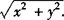

(7)若A(x₁，y₁)，B(x₂，y₂)，

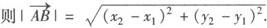
(8)若a=(x₁，y₁)，b=(x₂，y₂)，

则a⊥b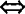x₁·x₂+y₁·y₂=0．

例1 已知：a、b都是非零向量且a+3b与7a—5b垂直，a—4b与7a—2b垂直，求a与b的夹角．

解 ∵(a+3b)⊥(7a—5b)，

且(a—4b)⊥(7a—2b)，

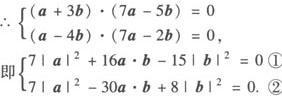
①—②得2a·b=|b|²， ③

③代入①得|a|²=|b|²，即|a|=|b|．

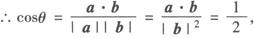
∴θ=60°．

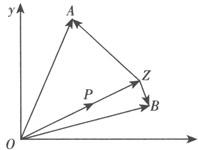
例2 如图，已知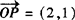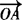，=(1，7)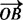，=(5，1)，设Z是直线OP上的一动点．

(1)求使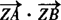取最小值的，

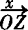(2)对(1)中求出的Z，求∠AZB．

解 (1)由题意，Z是直线OP上的一点

∴．

设实数t，使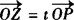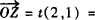，∴(2t，t)，

则

=(1—2t，7—t)．

．

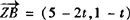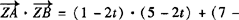∴t)(1—t)

=5t²—20t+12=5(t—2)²—8．

当t=2时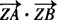，有最小值—8此时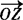=(4，2)．

(2)当t=2时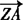，=(—3，5)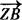，=(1，—1)．

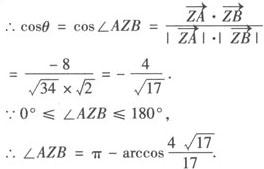
例3 若向量a=(1，1)，b=(1，—1)c=(—1，2)，则c=( )．

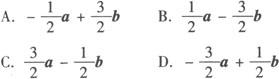
分析 本题考查了平面向量的基本定理及向量的坐标运算．

解 设c=λ₁a+λ₂b，则(—1，2)=λ₁(1，1)+λ₂(1，—1)=(λ₁+λ₂，λ₁—λ₂)．

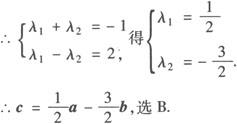
例4 已知平面上三点的坐标分别为A(—2，1)，B(—1，3)，C(3，4)，求点D的坐标，使这四个点构成平行四边形的四个顶点．

分析 注意到没有指明顶点的顺序，故应分类讨论，平行四边形的对边平行且相等，从而两个向量相等，故可求出D点坐标．

解 (1)以AC为一条对角线时得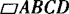，设D(x，y)，则由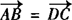得(—1+2，3—1)=(3—x，4—y)．

∴3—x=1，4—y=2．

∴x=2，y=2，即D(2，2)．

(2)以BC为一条对角线时得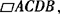设D(x，y)，则由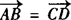

得(—1+2，3—1)=(x—3，y—4)．

∴x—3=1，y—4=2．

∴x=4，y=6，即D(4，6)．

(3)AB为一条对角线时得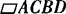，则由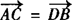同样求得D(—6，0)．

综上所述，当D的坐标为(2，2)或(4，6)或(—6，0)时，都能用这四个点构成平行四边形的四个顶点．

例5 设a、b、c是任意的非零平面向量，且它们相互不共线，下列命题

①(a·b)·c—(c·a)·b=0；

②|a|—|b|<|a—b|；

③(b·c)·a—(c·a)·b不与c垂直；

④(3a+2b)·(3a—2b)=9|a|²—4|b|²．

其中正确的是( )．

A．①② B．②③

C．③④ D．②④

解 选D．②正确，因a、b不共线，在|a|—|b|≤|a—b|中不能取等号；④正确是明显的；①错误，因向量的数量积不满足结合律；③错误，因[(b·c)·a—(c·a)·b]·c=(b·c)·(a·c)—(c·a)·(b·c)=0，则(b·c)·a—(c·a)·b与c垂直．