证明的一般步骤

出处：按学科分类—文体、科学、教育 商务印书馆国际有限公司《初中数理化公式定理大全》第142页（2115字）

1．理解题意．

2．根据题意正确画出图形．

3．根据题意写出已知和求证．

4．分析题意，探索证明思路．

5．根据寻求的思路，运用数学符号和数学语言条理清晰地写出证明过程．

6．检查表达过程是否正确，完善．

注意 在寻求思路的过程中，可以从已知向求证探索，也可以倒过来从求证向已知追溯，还可以从已知和求证两个方向出发，互相接近．

例1 如图所示，已知：AB∥CD，∠B=120°，CA平分∠BCD．

求证：∠1=30°．

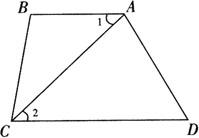
证明 ∵AB∥CD，(已知)

∴∠B+∠BCD=180°．(两直线平行，同旁内角互补)

∵∠B=120°，(已知)

∴∠BCD=60°．

又CA平分∠BCD，(已知)

∴∠2=1/2∠BCD=30°．(角平分线定义)

∵AB∥CD，(已知)

∴∠1=∠2=30°．(两直线平行，内错角相等)

例2 如图所示，已知AD⊥BC，垂足为D，EG⊥BC，垂足为G，EG交AB于F，且∠AFE=∠E，求证：AD平分∠BAC．

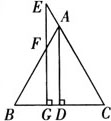
证明 ∵EG⊥BC，(已知)

∴∠EGB=90°．(垂直定义)

∴∠BFG+∠B=90°．(三角形内角和定理)

∵∠BFG=∠AFE，(对顶角相等)

∴∠AFE+∠B=90°．(等量代换)

又∵∠AFE=∠E，(已知)

∴∠B+∠E=90°．(等量代换)

又∵EG⊥BC，(已知)

∴∠EGC=90°．(垂直定义)

∴∠E+∠C=90°．(三角形内角和定理)

∴∠B=∠C．(等量代换)

∴AB=AC．(等角对等边)

又∵AD⊥BC，(已知)

∴AD平分∠BAC．(等腰三角形三线合一)

例3 求证：如果两个三角形有两条边和其中一边上的中线对应相等，那么这两个三角形全等．

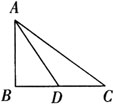
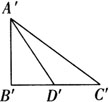
已知：如图，△ABC和△A′B′C′中，AB=A′B′，BC=B′C′，AD、A′D′分别为△ABC和△A′B′C′的中线且AD=A′D′．

求证：△ABC≌△A′B′C′．

证明 ∵BC=B′C′，BD=1/2BC，B′D′= 1/2B′C′，∴BD=B′D′．

在△ABD和△A′B′D′中

∵AB=A′B′，BD=B′D′，AD=A′D′∴△ABD≌△A′B′D′．(SSS)

∴∠B=∠B′，在△ABC和△A′B′C′中，∵AB=A′B′，∠B=∠B′，BC=B′C′．

∴△ABC≌△A′B′C′．(SAS)

[解析] 文字证明题，首先要找到这个命题的题设和结论，审清题意，正确画出图形，然后再结合图形写出已知，求证，最后进行证明．