粗大误差

出处：按学科分类—工业技术 企业管理出版社《计量专业工程师手册》第89页（1793字）

粗大误差明显歪曲了测量结果。含粗差的测量值是异常值，应予舍去。

工作仔细，加强责任心，可以防止粗大误差。

测量进行中若发现有的条件不符合要求，可以当场抛掉当时所测数据，即将该值在记录中划去，但须注明原因。不说明原因而随意抛掉一个数据是不正确的。

测量进行后，要判断一个数是否含有粗大误差要特别慎重，此时应根据充分的测量知识和下面的粗大误差准则，作为剔除的根据。

设对某量作等精度独立测量，得

x₁，x₂，…，x_n

算出平均值及残差

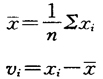
按贝塞尔法算单次测量标准差

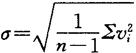
此时剔除粗大误差的准则有：

1．来伊达准则

如果某测量值x_i之

｜v_i｜＞3σ (2．5－1)

则认为x_i含粗大误差而抛去。

〔例2．5－1〕 测某一温度15次，得x_i如表2．5－1。

表2．5－1 测温数据

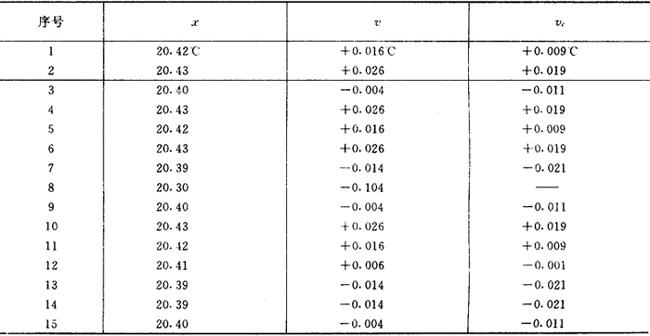
120．404℃

120．404℃

今

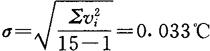
而｜v₈｜=0．104℃＞3σ=0．099℃

故将x₈舍去。舍去后再算平均值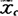及

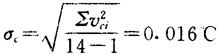
由3σ_c判断，知新列中已无粗大误差。

来伊达准则宜n＞10。

2．格拉布斯(Grubbs)准则

若测量值的最大值或最小值有满足

｜v_i｜＞λ_n(α)·σ (2．5－2)

则认为含粗大误差而剔去。

系数λ_n(α)与测量次数n及显着信水平α有关，其值见表2．5－2。

表2．5－2 拉布斯系数λ_n(α)

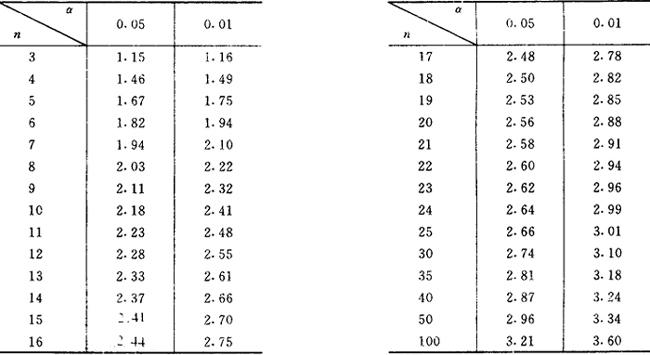
【参考文献】：

［1］王立吉，计量学基础，中国计量出版社，1988。

［2］BIPM、IEC、IFCC，IUPAC，IUPAP，OIML，Guide to the Expression of Uncertainty in Measurement， ISO，1993．

［3］刘智敏，不确定度原理，中国计量出版社，1993。

［4］刘智敏，误差分布论，原子能出版社，1988。

［5］刘智敏，误差与数据处理，原子能出版社，1983。

［6］Liu Zhimin(刘智敏)，Measurement Uncertainty and Its Correlation Combination，Proceeding of ISEM， 1993．

［7］国家计量总局量值传递处编，计量技术考核纲要，计量出版社，1981。

［8］国家技术监督局审定，刘智敏等编审，全国计量检定人员考核统一试题集第六分册三，误差及数据处理，陕西科学技术出版社，1990。