误差的检验和减免
出处:按学科分类—农业科学 农业出版社《土壤农化分析手册》第35页(1721字)
为提高测定方法的准确度和测定结果的可靠性,应对误差进行检验,并进一步采用各种方法,使误差减免至最小,达到允许误差的范围。一般可采用下列方法:
(一)对试验用仪器、器皿及试剂进行检验和校正 各种计量测试仪器,如天平、砝码、温度计、分光光度计等,应按规定定期由计量管理部门检定,以保证仪器的灵敏度和准确度。使用的标准容量器如滴定管、移液管等,最好经过标定,按校正值使用。各种试剂应按规格使用;标准溶液要按规定定期标定,以保证试剂的质量和浓度。
(二)增多测定次数 一般来说,测定次数愈多,则平均值越接近真实值,偶然误差可以抵消。但测定次数太多浪费太大,而且往往是不必要的。一般每个样品可平行测定二次,误差在允许范围内,取其平均值计算。若误差较大,则应增加1或2次。要求精密的测定,还可增加测定次数。利用多测可减免偶然误差,并往往可以检验出误差来源。
(三)空白试验 在测定同时作空白试验,然后在测定值中扣除空白值,就可以减免许多尚不明了的因素产生的误差。
(四)对照试验 用标准样品(或称参比样品)进行对照试验;或者用标准方法(或称参比方法)进行对照;或者由本单位不同人员或不同单位进行分析对照试验,都可以检验和校正分析结果的误差。
(五)回收率试验 用已知量待测成分的标准物质按照所定操作步骤和条件进行测定,计算回收率:
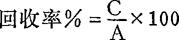
C为实际测得的标准物质量;
A为加入的标准物质量。
回收率可以检验分析方法的准确度和样品所引起的干扰误差,并可同时求出精确度。
还可以将已知量的待测成分标准物加入样品中,与另一份样品同时测定,由二者之差与已知加入量计算回收率,此法常称为“标准加入法”,所得结果则更可靠。
(六)作工作曲线及回归方程 在用比色、荧光、火焰光度、原子吸收分光光度等方法分析时,常常需要制备一系列标准溶液,测定其参数(吸收值、荧光强度、峰高等)绘制其与标准溶液浓度之间的关系曲线,称为工作曲线,这是最常用的一种方法。但有时工作曲线的点阵往往不在一直线上,此时可用回归法求出该线的方程,就能最合理地代表此工作曲线。
一般将物质的含量或浓度作为变数(x),标绘在横坐标上;测得的参数作因变数(y),标绘在纵坐标上。根据最小二乘法原理,计算出直线方程的截距b和斜率a之值:

式中:n——测定的次数;
x——物质的含量或浓度(即变数),为横坐标;
y——测得的参数(即因变数),为纵坐标。
则回归后的直线方程为:y=ax+b
也可以由上二式中任一式求得a或b后,代入y=ax+b方程式,然后求出b或a来。
例:马铃薯块茎中淀粉含量(以x代表)和其比重(以y代表)的测定结果如下表:

代入下式求a:

代入下式求b:
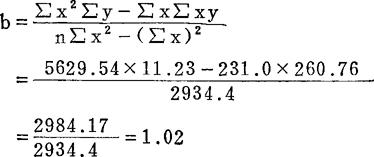
则y=0.0005x+1.02为回归方程。
或用下式求b:

则y=0.005x+1.01为回归方程。
利用回归方法不仅可求出平均的直线方程式,还可以检验结果的可靠性。