以置信度1—a区间估计正态总体的标准差、平均数及取值
出处：按学科分类—农业科学 农业出版社《水产养殖手册》第893页（1779字）
本章第三—七节的内容主要适用于正态总体(及其族)，对于一般的总体(及其族)按照本章内容进行统计计算与分析，应该使用大样本(n>100)。
正态总体的标准差与平均数都是客观存在的未知常数，可以用样本的差异平方和，方差与平均数这三个统计量的观测值Ssx，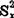
，
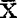，配合显着性检验的临界值(又称为分位数)uα，
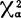(f)，tα(f)，Fα(f1，f2)，rα(f)，等，对它们进行区间估计，如同(48．3．6)式以及(48．4．5—9)式所表示的那样。估计的误差范围和可靠性分别用区间长度和置信度1—α表示。α称为信度，一般为小概率5%或者1%，是显着性检验的显着度(又称为显着水平)。表48—1中的r-检验，表48—2中的F-检验以及后面表48—4和表48—5中的X2-检验和F-检验，统计量的观测值大于α越小的临界值(分位数)，则差异越显着。
(1)正态总体X的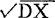
记为σ，EX记为μ。
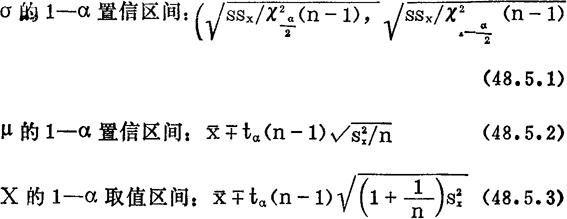
(2)两个(同种生物数量)相互独立的正态总体X1与X2的标准差，平均数，样本容量分别为：j，μj，nj，j=1，2。
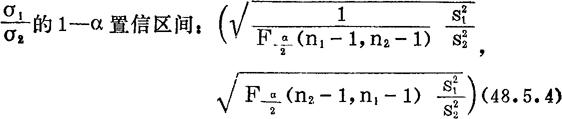
如果上述区间包含1在内，则可以近似地(误差不超过区间)认为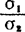
=1，即σ1=a2。这一结论的可靠性是1—α。μ1—μ2的1—α置信区间分为两种情形：
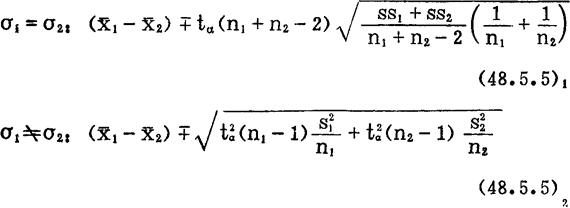
如果区间(48．5．5)1-2包含0在内，则可以近似地(误差不超过区间)认为μ1-μ2=0，即μ1=μ2，X1与X2差异不显着(随机差异)；如果不包含0在内，则μ1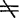
μ2，
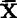1与X2差异显着(系统差异)，区间表示总体X1与X2取值之间平均的差异程度。以上结论的可靠性是1—α。对于σ1
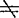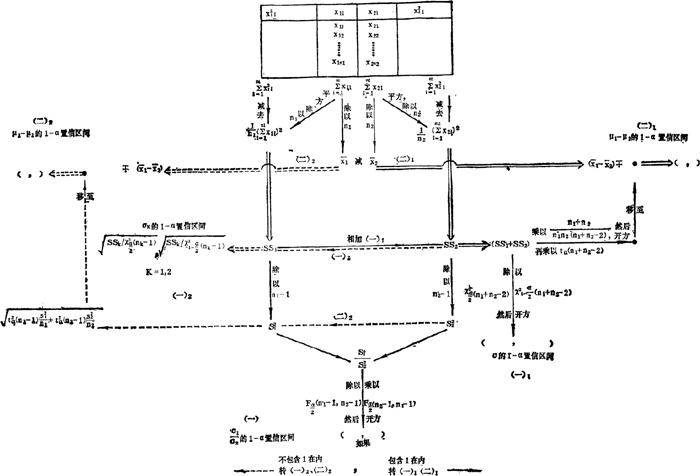
σ2以及μ1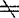
μ2的情形，需要按照(48．5．1)式以及(48．5．2)式分别计算σj与μj，j=1，2的1—α置信区间。表48—3给出了(48．5．4)式及其后继内容的计算步骤(表48—3附文后)。
表48—3 正态总体参数的1—a置信区间
(3)r个(同种生物数量)相互独立的正态总体Xk，k=1—r的方差齐性显着性检验：
r(r≥3)个相互独立的正态总体Xk，k=1—r分别在r种条件下产生。“条件”指生态(自然，实验，生产)条件，生物特性，单因子的水平，多因子的水平搭配等。如果因子是数量，则“水平”是数量因子的取值。
r个相互独立的正态总体Xk的样本容量分别为nk，k=1-r；样本观测值的平均数，差异平方和与方差分别为Xk，sSk与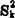
，k=1—r，并由它们构成随机平方和ss。与随机方差
：
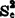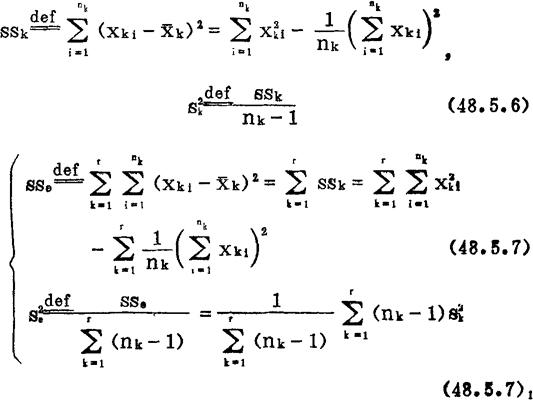
Bartlett(巴特莱)统计量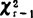
表示r个相互独立的正态总体的样本方差
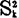，k=1—r之间的差异程度，其观测值定义如下：
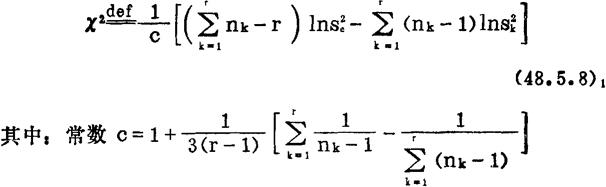
如果nk≡n，k=1—r，则上式转化为如下简单形式：
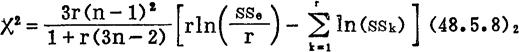
上式括号外的系数是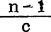
。
(48．5．8)1式的计算步骤如表48—4(1)(一)所示；(48．5．8)2式的计算步骤如表48—4(2)(一)和表48—6(一)所示。
如果X2<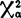
(r-1)，则r个
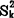，k=1—r之间的差异不显着(随机差异)，从而可以近似地认为
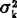≡σ2，k=1—r。这是回归分析和方差分析中F-检验步骤的前提。
(编者：刘长安 审者：孙尽善)