函数的极限

出处：按学科分类—数理科学和化学 清华大学出版社《数学手册（大学生用）》第31页（4206字）

自变量趋向有限值时函数的极限定义 设函数f(x)在点x₀的某一去心邻域内有定义．如果对于任意给定的正数ε，不论它多么小，总存在相应的正数δ，使得满足不等式0＜|x－x₀|＜δ的一切x，对应的函数值f(x)都满足不等式

|f(x)－A|＜ε，则称常数A为函数f(x)当x→x₀时的极限，记作

或f(x)→A(x→x₀)．

简述为“ε－δ”定义：，，使当0＜|x－x₀|＜δ时，恒有|f(x)－A |＜ε．(其中表示任意，表示存在．)

自变量趋向有限值时函数的极限几何意义 任意给定一正数ε，作平行于x轴的两条直线y=A+ε和y=A－ε，存在着点x₀的一个去心δ邻域，当x属于时，y=f(x)的图形位于这两直线之间(见图2．7)．

图2．7

左极限 ，，使当x₀－δ＜x＜x₀时，恒有|f(x)－A|＜ε，记作

右极限 ，，使当x₀＜x＜x₀+δ时，恒有|f(x)－A|＜ε，记作

定理

自变量趋向无穷大时函数的极限定义 如果对于任意给定的正数ε，总相应存在正数X，使得满足不等式|x|＞X的一切x，所对应的函数值f(x)都满足不等式|f(x)－A|＜ε，那么常数A就叫函数f(x)当x→∞时的极限，记作

几何意义 任意给定一正数ε，作平行于x轴的两条直线y=A+ε和y=A－ε，则总存在着一个正数X，使得当x＜－X或x＞X时，函数y=f(x)的图形位于这两直线之间(见图2．8)．

图2．8

1．的情形

任给ε＞0，存在X＞0，当x＞X时恒有

|f(x)－A|＜ε．

2．的情形

任给ε＞0，存在X＞0，当x＜－X时恒有

|f(x)－A |＜ε．

定理 且

水平渐近线 如果，则直线y=c是曲线y=f(x)的水平渐近线．

铅直渐近线 如果，则直线x=x₀是曲线y=f(x)的铅直渐近线．

极限的局部保号性定理

(1)如果，而且A＞0(或A＜0)，那么就存在着点x₀的某一去心邻域，当x在该邻域内时，就有f(x)＞0(或f(x)＜0)．

(2)如果，那么就存在着x₀的某一去心邻域，当时，就有．

(3)如果在x₀的某一去心邻域内f(x)≥0(或f(x)≤0)而且，那么A≥0(或A≤0)．

说明：以下记号“lim”是指对x→x₀及x→∞都成立．

无穷小定义 若limf(x)=0，则称函数f(x)当x→x₀(或x→∞)时为无穷小．

无穷小与函数极限的关系定理 ，其中α(x)是当x→x₀(或x→∞)时的无穷小．

无穷大定义 若limf(x)=∞(指）(或|x|＞N，N为某一正数)时，|f(x)|＞M，M为任意正数)，则称函数f(x)当x→x₀(或x→∞)时为无穷大．

正无穷大和负无穷大的定义 limf(x)=+∞(或limf(x)=－∞)．(指f(x)＞M(或f(x)＜－M)，M为任意正数．)

无穷小与无穷大的关系定理 若limf(x)=0(f(x)≠0)，则反之也成立．

定理 有限个无穷小的和也是无穷小(注意：无穷多个无穷小的代数和未必是无穷小)．

定理 有界函数与无穷小的乘积是无穷小．

定理 常数与无穷小的乘积是无穷小．

定理 有限个无穷小的乘积也是无穷小．

极限的四则运算定理 设limf(x)=A，limg(x)=B，则

定理 如果limf(x)存在，且c为常数，则

lim［cf(x)］=climf(x)．

定理 如果limf(x)存在，且n是正整数，则

lim［f(x)］ⁿ=［limf(x)］ⁿ．

局部不等性定理 如果φ(x)＞ψ(x)，且limφ(x)=a，limψ(x)=b，则a≥b．

复合函数的极限运算法则 设函数u=φ(x)当x→x₀时的极限存在且等于a，即，但在点x₀的某去心邻域内φ(x)≠a，又，则复合函数f［φ(x)］当x→x₀时的极限也存在，且

夹逼准则Ⅰ 如果数列x_n，y_n及z_n满足下列条件

y_n≤x_n≤z_n(n=1，2，3，…)，

且，，那么数列x_n的极限存在，且．

夹逼准则Ⅱ 如果当(或|x|＞M)时，有

g(x)≤f(x)≤h(x)，

且limg(x)=A，limh(x)=A，那么limf(x)存在，且等于A．

单调数列

1．如果数列｛x_n｝满足条件

x1≤x₂≤…≤x_n≤x_n+1≤…，

就称数列｛x_n｝是单调递增数列．

2．如果数列｛x_n｝满足条件

x₁≥x₂≥…≥x_n≥x_n+1≥…，

就称数列｛x_n｝是单调递减数列．

单调递增数列和单调递减数列统称为单调数列．

单调有界准则 单调有界数列必有极限．

柯西极限存在准则(柯西收敛原理) 数列｛x_n｝收敛的充分必要条件是对于任意给定的正数ε，存在着这样的正整数N，使得当m＞N，n＞N时，恒有|x_n－x_m|＜ε．

两个重要极限

无穷小的比较 设α，β是同一过程中的两个无穷小，且α≠0．

(1)如果，就说β是α的高阶无穷小，记作β=o(α)．

(2)如果，就说β是α的低阶无穷小．

(3)如果l，就说β与α是同阶无穷小．特殊地，如果，则称β与α是等价无穷小．记作α～β．

(4)如果l，就说β是α的k阶无穷小．

常见的等价无穷小(以下等价无穷小均是在x→0时的情况)

sinx～x，arcsinx～x，tanx～x，arctanx～x，

ln(1+x)～x，．

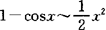等价无穷小代换定理

(1)设α～α′，β～β′，且l存在(或无穷大)，则l存在(或无穷大)，且

(2)设α～α′，β～β′，且l存在(或无穷大)，则存在(或无穷大)，且

(3)设α～α′，β～β′，γ～γ′，且l，则

定理 β与α是等价无穷小的充分必要条件为β=α+o(α)．