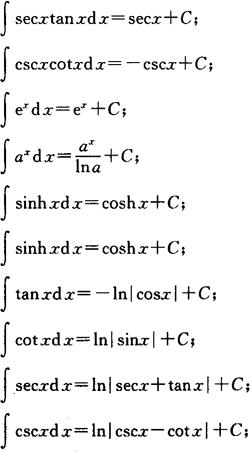不定积分

出处：按学科分类—数理科学和化学 清华大学出版社《数学手册（大学生用）》第72页（2293字）

原函数 如果在区间I内，可导函数F(x)的导函数为f(x)，即对任一x∈I，都有

F′(x)=f(x) 或 dF(x)=f(x)dx，

则函数F(x)就称为f(x)在区间I内的原函数．

原函数存在定理 如果函数f(x)在区间I上连续，那么在区间I上存在可导函数F(x)，使对任一x∈I，都有

F′(x)=f(x)．

简言之，连续函数一定有原函数．

不定积分定义 如果在区间I上，F(x)是f(x)的一个原函数，则F(x)+C称为f(x)在区间I上的不定积分，记为

∫f(x)dx．

其中记号∫称为积分号，f(x)称为被积函数，f(x)dx称为被积表达式，x称为积

分变量．

积分曲线 函数y=f(x)的原函数的图形称为f(x)的积分曲线．显然，不定积分得到的是积分曲线族．

不定积分的性质

(1)∫［f(x)±g(x)］dx=∫f(x)dx±∫g(x)dx

(此性质可推广到有限多个函数之和的情况)．

(2)∫kf(x)dx=k∫f(x)dx(k是常数，k≠0)．

第一类换元积分法 设|f(x)dx=F(x)+C，则

|f［φ(x)］φ′(x)dx=F(φ(x))+C，

其中φ(x)是可微函数，简记为

|f(u)du=F(u)+C．

由此可见，已知公式中的x换为可微函数φ(x)，公式仍成立．

例 已知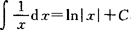所以

第二类换元积分法 设x=ψ(t)是单调的、可导的函数，并且ψ′(t)≠0．又设f［ψ(t)］ψ′(t)具有原函数，则有换元公式

其中ψ(x)是x=ψ(t)的反函数．

第二类换元积分法主要解决的问题

被积函数中含有根式的积分问题．

解 令x=atant，则，于是

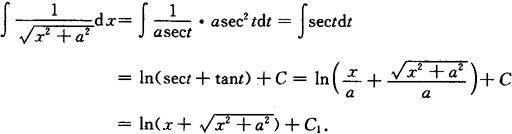
分部积分法

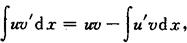
或写为

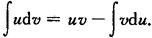
分部积分法的特点 等号两边的积分中u与v交换位置．

例1 求∫lnxdx．

解

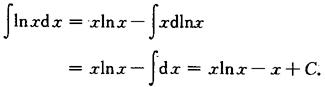
例2 求|xlnxdx．

解 要凑一个微分，再用分部积分法．

下列类型可用分部积分法解决：

其中p(x)为x的多项式．

有理函数积分法 有理函数分解为多项式及最简分式之和后，各个部分都能积出，且原函数都是初等函数．

三角有理式的定义 由三角函数和常数经过有限次四则运算构成的函数称之为三角有理式，一般记为R(sinx，cosx)．

三角函数有理式积分法

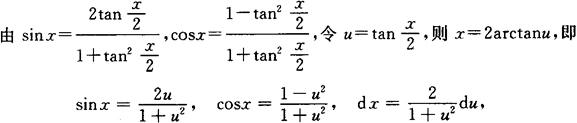
则三角有理式R(sinx，cos．x)的积分可化为

例 求．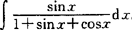

解 令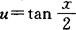，则

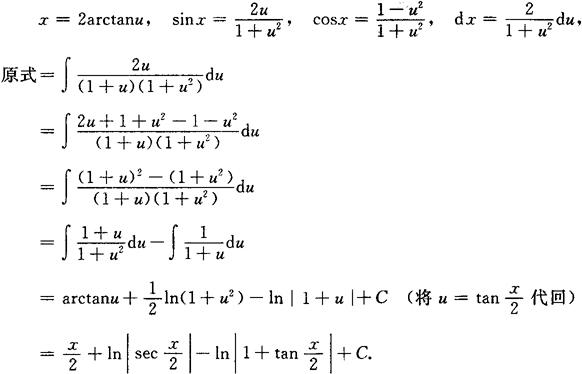
基本积分表