定积分
出处:按学科分类—数理科学和化学 清华大学出版社《数学手册(大学生用)》第82页(3107字)
定积分定义 设函数f(x)在[a,b]上有界,在[a,b]中任意插入n-1个分点
a=x0<x1<x2<…<xn-1<xn=b,
把区间[a,b]分成n个子区间,
[x0,x1],[x1,x2],…,[xn-1,xn],
各子区间的长度依次为
△xi=xi-xi-1, (i=1,2,…,n),
在各子区间[xi-1,xi]上任取一点ξi(ξi∈[xi-1,xi]),作乘积
f(ξi)△xi (i=1,2,…,n),
并作和

记λ=max{△x1,△x2,…,△xn},如果不论对[a,b]怎样的分法,也不论在小区间[xi-1,xi]上点ξi怎样的取法,只要当λ→0时,和S总趋于确定的极限I,则称这个极限I为函数f(x)在区间[a,b]上的定积分,记为 即
即

其中f(x)叫做被积函数,f(x)dx叫做被积表达式,x叫做积分变量,a叫做积分下限,b叫做积分上限,[a,b]叫做积分区间,和 i称为积分和.如果
i称为积分和.如果
f(x)在[a,b]上的定积分存在,则说f(x)在[a,b]上可积.
定积分存在定理1 当函数f(x)在[a,b]上连续时,f(x)在区间[a,b]上可积.
定积分存在定理2 设函数f(x)在区间[a,b]上有界,且只有有限个第一类间断点,则f(x)在区间[a,b]上可积.
定积分的几何意义

其中A1,A2,A3表示图中所示的面积(见图6.1).

图6.1
定积分的补充规定

定积分的性质(在下面的定积分的性质中,假定定积分都存在)
(1) (此性质可以推广到有限多个函数和的情况).
(此性质可以推广到有限多个函数和的情况).
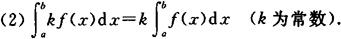
(3)不论a,b,c的相对位置如何,则

(5)如果在区间[a,b]上f(x)≥0,则

推论 如果在区间[a,b]上f(x)≤g(x),则

(6)设M及m分别是函数f(x)在区间[a,b]上的最大值及最小值,则

(此性质可用于估计积分值的范围).
定积分的中值定理(或积分中值公式) 如果函数f(x)在闭区间[a,b](或[b,a])上连续,则在积分区间[a,b](或[b,a])上至少存在一个点ξ,使
 (ξ在a与b之间,b不一定要大于a).
(ξ在a与b之间,b不一定要大于a).
定积分中值定理的几何解释 在区间[a,b]上至少存在一个点ξ,使得以区间[a,b]为底边,以曲线y=f(x)为曲边的曲边梯形的面积等于同一底边长乘高为f(ξ)的一个矩形的面积(见图6.2).

图6.2
上限为变量的定积分(变上限定积分)
设函数f(x)在区间[a,b]上连续,并且设x为[a,b]上的一点,则称积分

为变上限的定积分.
变上限的定积分的导数定理(或原函数存在定理) 如果函数f(x)在[a,b]上连续,则函数

在[a,b]上具有导数,且它的导数是

即 t就是f(x)在[a,b]上的一个原函数
t就是f(x)在[a,b]上的一个原函数
特别地,如果f(t)连续,a(x),b(x)可导,则

的导数F′(x)为

牛顿-莱布尼茨公式(微积分基本公式) 如果函数F(x)是连续函数f(x)在区间[a,b]上的一个原函数,则

记为

(当a>b时,公式仍成立.)
微积分基本公式表明:
(1)一个连续函数在区间[a,b]上的定积分等于它的任意一个原函数在区间[a,b]上的增量;
(2)求定积分问题转化为求原函数的问题.
定积分的换元法 假设函数f(x)在[a,b]上连续,函数x=φ(t)在[α,β]上是单值的且有连续导数,当t在区间[α,β]上变化时,x=φ(t)的值在[a,b]上变化,且φ(α)=a,φ(β)=b,则有定积分的换元公式
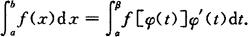
当α>β时,换元公式仍成立.
例 计算
解 令t=cos.x,则dt=-sinxdx,
当 时,t=0,当x=0时,t=1,故
时,t=0,当x=0时,t=1,故

定积分的分部积分法 设函数u(x),v(x)在区间[a,b]上具有连续导数,则有定积分的分部积分公式

简记为

定积分常用公式
