多元函数

出处：按学科分类—数理科学和化学 清华大学出版社《数学手册（大学生用）》第133页（3025字）

邻域 设P₀(x₀，y₀)是Oxy平面上的一个点，δ是某一正数，与点P₀(x₀，y₀)距离小于δ的点P(x，y)的全体，称为点P₀的δ邻域，记为U(P₀，δ)，即

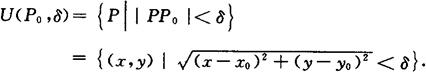
内点 设E是平面上的一个点集，P是平面上的一个点．如果存在点P的某一邻域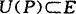，则称P为E的内点．

开集 如果点集E的点都是内点，则称E为开集．

例如：E₁=｛(x，y)|1＜x²+y²＜4｝即为开集．

边界点 如果点P的任一个邻域内既有属于E的点，也有不属于E的点(点P本身可以属于E，也可以不属于E)，则称P为E的边界点．

E的边界点的全体称为E的边界．

连通 开集D内任何两点，都可用折线连结起来，且该折线上的点都属于D，则称开集D是连通的．

连通的开集称为区域或开区域．

例如：｛(x，y)1＜x²+y²＜4｝．

开区域连同它的边界一起称为闭区域．

例如：｛(x，y)1≤x²+y²≤4｝．

有界点集 对于点集E，如果存在正数K，使一切点P∈E与某一定点A间的距离|AP|不超过K，即

|AP|≤K，

则称E为有界点集，否则称为无界点集．

例如：｛(x，y)|1≤x²+y²≤4｝为有界闭区域，｛(x，y)|x+y＞0｝为无界开区域．

聚点 设E是平面上的一个点集，P是平面上的一个点，如果点P的任何一个邻域内总有无限多个点属于点集E，则称P为E的聚点．

内点一定是聚点；边界点可能是聚点．

例如：｛(x，y)|0＜x²+y²≤1｝，(0，0)既是边界点，也是聚点．

点集E的聚点可以属于E，也可以不属于E．

n维空间 设n为取定的一个自然数，我们称n元数组(x₁，x₂，…，x_n)的全体为n维空间，而每个n元数组(x₁，x₂，…，x_n)称为n维空间中的一个点，数x_i称为该点的第i个坐标，n维空间的记号为Rⁿ．

n维空间中两点间的距离公式 n维空间中两点为P(x₁，x₂，…，x_n)，Q(y₁，y₂，…，y_n)，则

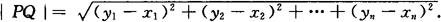
当n=1，2，3时，便为数轴、平面、空间两点间的距离．

n维空间中邻域定义 U(P₀，δ)=｛P||PP₀|＜δ，P∈Rⁿ｝

二元函数 设D是平面上的一个点集，如果对于每个点P(x，y)∈D，变量z按照一定的法则总有确定的值和它对应，则称z是变量x，y的二元函数，记为z=f(x，y)(或记为z=f(P))．

类似地可定义三元及三元以上函数．

当n≥2时，n元函数统称为多元函数．多元函数中同样有定义域、值域、自变量、因变量等概念．

二元函数z=f(x，y)的图形 设函数z=f(x，y)的定义域为D，对于任意取定的P(x，y)∈D，对应的函数值为z=f(x，y)，这样，以x为横坐标、y为纵坐标、z为竖坐标在空间就确定一点M(x，y，z)，当x取遍D上一切点时，得一个空间点集｛(x，y，z)|z=f(x，y)，(x，y)∈D｝，这个点集称为二元函数的图形．二元函数的图形通常是一张曲面(如图9．1)．

图9．1

二元函数的极限 设函数z=f(x，y)的定义域为D，P₀(x₀，y₀)是其聚点，如果对于任意给定的正数ε，总存在正数δ，使得对于适合不等式

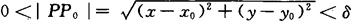
的一切点，都有|f(x，y)－A|＜ε成立，则称A为函数z=f(x，y)当x→x₀，y→y₀时的极限，记为

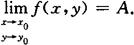
(或f(x，y)→A(ρ→0)，这里ρ=|PP₀|)．为了区别于一元函数的极限，我们把二元函数的极限叫做二重极限．

确定二元函数的极限不存在的方法 令P(x，y)沿y=kx趋向于P₀(x₀，y₀)，若极限值与k有关，则可断言极限不存在．

找两种不同的趋近方式，使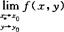存在，但两者不相等，此时也可断言f(x，y)在点P₀(x₀，y₀)处极限不存在．

n元函数的极限定义 设n元函数f(P)的定义域为点集D，P₀是其聚点．如果对于任意给定的正数ε，总存在正数δ，使得对于适合不等式

0＜|PP₀|＜δ

的一切点P∈D，都有|f(P)－A|＜ε成立，则称A为n元函数f(P)当P→P₀时的极限，记为

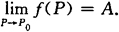
多元函数的连续性 设n元函数f(P)的定义域为点集D，P₀是其聚点且P₀∈D，如果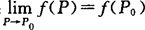则称n元函数f(P)在点P₀处连续．

设P₀是函数f(P)的定义域的聚点，如果f(P)在点P₀处不连续，则称P₀是函数f(P)的间断点．

多元初等函数 由多元多项式及基本初等函数经过有限次的四则运算和复合步骤所构成的可用一个式子所表示的多元函数叫多元初等函数．

一切多元初等函数在其定义区域内是连续的．

一般地，求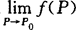时，如果f(P)是初等函数，且P₀是f(P)的定义域的内点，则f(P)在点P₀处连续，于是．

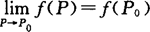定义区域 是指包含在定义域内的(开)区域或闭区域．