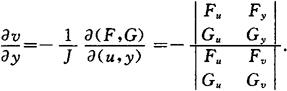偏导数

出处：按学科分类—数理科学和化学 清华大学出版社《数学手册（大学生用）》第139页（2682字）

偏导数的定义 设函数z=f(x，y)在点(x₀，y₀)的某一邻域内有定义，当y固定在y₀而x在x₀处有增量△x时，相应地函数有增量f(x₀+△x，y₀)－f(x₀，y₀)，如果

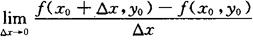
存在，则称此极限为函数z=f(x，y)在点(x₀，y₀)处对x的偏导数，记为

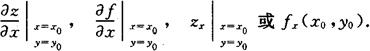
同理可定义函数z=f(x，y)在点(x₀，y₀)处对y的偏导数，

偏导函数的定义 如果函数z=f(x，y)在区域D内任一点(x，y)处对x的偏导数都存在，那么这个偏导数就是x、y的函数，它就称为函数z=f(x，y)对自变量x的偏导函数，记作

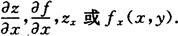
同理可以定义函数z=f(x，y)对自变量y的偏导函数，记作

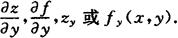
在不发生混淆时也称偏导函数为偏导数．

偏导数的概念可以推广到二元以上函数 如u=f(x，y，z)在(x，y，z)处

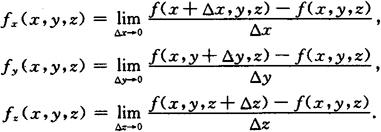
偏导数的几何意义 设M₀(x₀，y₀，f(x₀，y₀))为曲面z=f(x，y)上一点(如图9．2)．

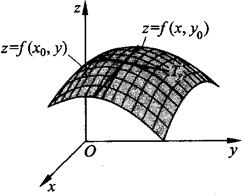
图9．2

偏导数f_x(x₀，y₀)就是曲面被平面y=y₀所截得的曲线在点M₀处的切线Tx的斜率．

偏导数f_y(x₀，y₀)就是曲面被平面x=x₀所截得的曲线在点M₀处的切线T_y的斜率．

高阶偏导数 函数z=f(x，y)的二阶偏导数为

二阶及二阶以上的偏导数统称为高阶偏导数．

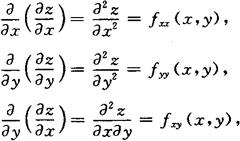
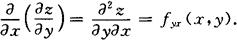
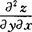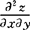定理 如果函数z=f(x，y)的两个二阶混合偏导数及在区域D内

连续，则在该区域内这两个二阶混合偏导数必相等．

多元复合函数链式求导法则

(1)如果函数u=φ(t)及v=ψ(t)都在点t可导，函数z=f(u，v)在对应点(u，v)具有连续偏导数，则复合函数z=f［φ(t)，ψ(t)］在对应点t可导，且其导数公式为(中间变量是二元函数)：

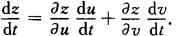
以上定理的结论可推广到中间变量多于两个的情况，如：

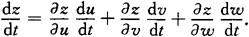
以上公式中的导数称为全导数．

(2)如果u=φ(x，y)及v=ψ(x，y)都在点(x，y)具有对x和y的偏导数，且函数z=f(u，v)在对应点(u，v)具有连续偏导数，则复合函数z=f［φ(x，y)，ψ(x，y)］在对应点(x，y)的两个偏导数都存在，且其偏导数公式为

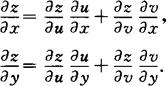
隐函数存在定理

(1)F(x，y)=0

隐函数存在定理1 设函数F(x，y)在点P(x₀，y₀)的某一邻域内具有连续的偏导数，且F(x₀，y₀)=0，Fy(x₀，y₀)≠0，则方程F(x，y)=0在点P(x₀，y₀)的某一邻域内惟一确定一个单值连续且具有连续导数的函数y=f(x)，它满足条件y₀=f(x₀)，并有

(2)F(x，y，z)=0

隐函数存在定理2 设函数F(x，y，z)在点P(x₀，y₀，z₀)的某一邻域内有连续的偏导数，且F(x₀，y₀，z₀)=0，F_z(x₀，y₀，z₀)≠0，则方程F(x，y，z)=0在点P(x₀，y₀，z₀)的某一邻域内惟一确定一个单值连续且具有连续偏导数的函数z=f(x，y)，它满足条件z₀=f(x₀，y₀)，并有

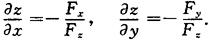
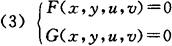
隐函数存在定理3 设F(x，y，u，v)，G(x，y，u，v)在点P(x₀，y₀，u₀，v₀)的某一邻域内有对各个变量的连续偏导数，且

F(x₀，y₀，u₀，v₀)=0，G(x₀，y₀，u₀，v₀)=0，

且偏导数所组成的函数行列式(或称雅可比式)

在点P(x₀，y₀，u₀，v₀)不等于零，则方程组

F(x，y，u，v)=0，G(x，y，u，v)=0

在点P(x₀，y₀，u₀，v₀)的某一邻域内惟一确定一组单值连续且具有连续偏导数的函数

u=u(x，y)，v=v(x，y)，

它们满足条件

u₀=u(x₀，y₀)，v₀=v(x₀，y₀)，

并有