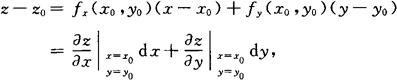全微分
出处：按学科分类—数理科学和化学 清华大学出版社《数学手册（大学生用）》第146页（1499字）
全增量 如果函数z=f(x，y)在点P(x，y)的某邻域内有定义，并设P′(x+△x，y+△y)为这邻域内的任意一点，则称这两点的函数值之差
f(x+△x，y+△y)－f(x，y)
为函数在点P对应于自变量增量△x，△y的全增量，记为△z，即
△z=f(x+△x，y+△y)－f(x，y)．
全微分 如果函数z=f(x，y)在点(x，y)的全增量
△z=f(x+△x，y+△y)－f(x，y)
可以表示为
△z=A△x+B△y+o(ρ)，
其中A，B不依赖于△x，△y而仅与x，y有关，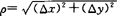
，则称函数z=f(x，y)在点(x，y)可微分，
A△x+B△y
称为函数z=f(x，y)在点(x，y)的全微分，记为dz，即
dz=A△x+B△y，
其中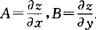
．
习惯上，记全微分为
全微分的定义可推广到三元及三元以上函数，三元函数的全微分记为
通常我们把二元函数的全微分等于它的两个偏微分之和这件事称为二元函数的微分符合叠加原理．叠加原理也适用于二元以上函数的情况．
若函数在区域D内各点处都可微分，则称这函数在D内可微分．
可微与连续关系定理 如果函数z=f(x，y)在点(x，y)可微分，则函数在点(x，y)连续．
可微的必要条件 如果函数z=f(x，y)在点(x，y)可微分，则该函数在点(x，y)的偏导数
必存在，且函数z=f(x，y)在点(x，y)的全微分为
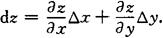
可微的充分条件 如果函数x=f(x，y)的偏导数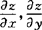
在点(x，y)连续，则该函数在点(x，y)可微分．
全微分形式不变性 设函数z=f(u，v)具有连续偏导数，则有全微分
当u=φ(x，y)，v=ψ(x，y)时，有
全微分形式不变形的实质：无论z是自变量u，v的函数或中间变量u、v的函数，它的全微分形式是一样的．
全微分的几何意义 因为曲面在M处的切平面方程为
