高阶线性微分方程

出处：按学科分类—数理科学和化学 清华大学出版社《数学手册（大学生用）》第242页（4950字）

二阶齐次线性微分方程的通解定理 形如

的方程称为n阶非齐次线性微分方程，a_i(x)(i=1，…，n)为已知函数．当f(x)恒为0时，即

y⁽ⁿ⁾+a1(x)y^(n－1)+a₂(x)y^(n－2)+…+a_n－1(x)y′+a_n(x)y=0

称为n阶齐次线性微分方程，当n=2时，为

yn+a₁(x)y′+a₂(x)y=0．

二阶齐次线性微分方程的一些结论．适用于n阶齐次线性微分方程．

同样，二阶非齐次线性微分方程的一些结论也适用于n阶非齐次线性微分方程．

如果y₁(x)与y₂(x)是方程

y′+a₁(x)y′+a₂(x)y=0

的解，则y=c₁y₁(x)+c₂y₂(x)也是方程的解，其中c₁，c₂是任意常数．当y₁(x)与y₂(x)线性无关时，则y=c₁y₁(x)+c₂y₂(x)是y″+a₁(x)y′+a₂(x)y=0的通解．

y1(x)与y₂(x)线性无关是指：在区间I上，如果存在不同时为零的常数λ，μ，使λy₁(x)+μy₂(x)=0，则称y₁(x)，y₂(x)在I上线性相关；否则，称y₁(x)，y₂(x)在I上线性无关．

二阶齐次线性微分方程解的求法 设y₁(x)是二阶齐次线性微分方程的解，则另一个与之线性无关的特解为

由此可得该二阶齐次线性微分方程的通解y=c₁y₁(x)+c₂y₂(x)．

二阶非齐次线性微分方程通解的结构定理 如果Y(x)是二阶非齐次线性微分方程

y″+a₁(x)y′+a₂(x)y=f(x)

的一个解，且c₁y₁(x)+c₂y₂(x)是其对应的齐次方程

y″+a₁(x)y′+a₂(x)y=0

的通解，则二阶非齐次线性微分方程的通解是

y=Y(x)+c₁y₁(x)+c₂y₂(x)．

二阶非齐次线性微分方程一个特解的求法 设y₁，y₂是二阶齐次线性微分方程的两个线性无关的解，那么二阶非齐次线性微分方程的特解为

y=c₁(x)y₁+c₂(x)y₂，

其中c₁(x)，c₂(x)是下列方程组的解：

例 求解方程y″+y=secx的通解．

解 显然sinx，cosx是二阶齐次方程y″+y=0的两个线性无关的解，设其特解为Y=c₁(x)sinx+c₂(x)cosx，其中c₁(x)，c₂(x)是下列方程组的解：

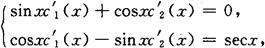
解得c′₁(x)=1，c′₂(x)=－tanx．各取一个原函数c₁(x)=x，c₂(x)=ln|cos．x|，所以原方程的通解为

y=c₁sinx+c₂cosx+cosxln|coSx|．

二阶常系数齐次线性微分方程的通解 设二阶常系数齐次线性微分方程是

y″+a1y′+a2y=0，

其中a₁，a₂为常数．其通解为

(1)当特征方程r²+a₁r+a₂=0有两个不相等的实根m₁，m₂时，方程通解为

y=c₁e^m1^x+c2e^m2^x．

(2)当特征方程r²+a₁r+a₂=0有重根m₁=m₂=m时，其通解为

y=(c₁rc₂x)e^mx．

(3)当特征方程r²+a₁r+a₂=0有复根m₁=α+iβ，m₁=α－iβ时，其通解为

y=(c₁cosβx+c₂sinβx)e^αx．

n阶常系数齐次线性微分方程的通解 设n阶常系数齐次线性微分方程为

y⁽ⁿ⁾+a1y^(n－1)+a2y^(n－2)+…+a_n－1y′+a_ny=0．

其特征方程为

rⁿ+a_n－1r^n－1+…+a_n－1r+a_n=0，

其中a_i(i=1，…，n)为常数．

其通解的构成如下：

(1)特征方程每一个实单根m对应着一个特解e^mx．

(2)特征方程每一个单共轭复根α±iβ，对应着两个特解：

e^αxcosβx，e^αxsinβx．

(3)特征方程每一个r重实根m对应着r个特解：

e^mx，xe^mT，x²e^mx，…，x^r－1e^mx．

(4)特征方程每一个r重共轭复根α±iβ，对应着2r个特解：

e^αxcosβx，e^αxsinβx，xe^αxcosβx，xe^αxsinβx，…x^r－1e^αxcosβx，x^r－1e^αxcosβx．

例 求方程的通解．

解 特征方程为

r⁵+r⁴+2r³+2r²+r+1=0，

即

(r+1)(r²+1)²=0．

特征方程有5个根：－1是实单根，±i是二重复根，所以通解为

y=c₁e^－x+(c₂+c₃x)cosx+(c₄+c₅x)sinx．

二阶常系数非齐次线性微分方程的一个特解求法

(1)当．f(x)=e^λxP_m(x)时，λ为常数，P_m(x)为x的m次多项式．则其特解为

y=x^ke^λxQ_m(x)， (1)

其中Q_m(x)为x的m次待定多项式，如果λ不是其特征方程的根取k=0；λ是特征根时，k等于特征根的重数．

将(1)式代入原方程，使之恒等定出Q_m(x)，从而得到原方程的特解．

(2)当．f(x)=e^λx(Pl(x)cosωx+P_n(x)sinωx)时，λ为常数，P_l(x)，P_n(x)分别为x的l次和n次的多项式，其特解为，

其中，均为x的t次多项式，且t=max(l，n)，如果λ+iω不是其特征方程根时，取k=0，否则取k等于特征根λ+iω的重数．

欧拉方程 形如

xⁿy⁽ⁿ⁾+a₁x^n－1y(^n－1)+…+a_n－1xy^′+a_ny=f(x)

的方程称为n阶欧拉方程，其中a_i(i=1，2，…，n)为常数．

二阶欧拉方程为

x²y″+a₁xy′+a₂y=f(x)．

设x=e^′，则t=lnx，有，代入方程即可化常系数线性方程．

微分算子法 令，，，称D，D²，…，Dⁿ为微分算子，则

y⁽ⁿ⁾+a₁y^(n－1)+…+a_n－1y′+a_ny=f(x) (1)

可写为

Dny+a₁Dⁿ_－¹y+a₂D^n－2y+…+a_n－1Dy+a_ny=f(x)，

记作

(Dⁿ+a₁D^n－1+a₂D^n－2+…+a_n－1D+a_n)y=f(x)．

记 P_n(D)=Dn+a₁Dⁿ－1+…+a_n－1D+a_n，则n阶常系数非齐次微分方程可记为

P_n(D)y=f(x)．

P_n(D)称为算子D的n次多项式．算子D有下列规律：

(1)P_n(D)e^λx=e^λxP_n(λ)；

(2)P_n(D)Q(x)e^λx=e^λxP_n(D+λ)Q(x)；

(3)是积分符号，是连续两次积分等，其中f(x)为x的多项式．

(4)要化为D的升幂级数，其中f(x)为x的多项式．

微分算子法是求常系数非齐次线性微分方程的一个特解的方法．

例1 求y⁽⁴⁾+4y″=48x²的特解．

解 将方程写为算子形式：

(D¹+4D²)y=48x²，

做形式运算得

利用算子规则有特解

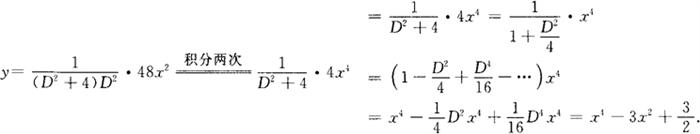
例2 求的特解．

解 写为算子形式，有

(D－3D－2)y=x³e^－x

因λ=－1是特征方程r³－3r－2=0的二重根，故设其特解为y=Q(x)e^－x，其中Q(x)为x的五次多项式，则

原方程为

e^－x(D－3)D²Q(x)=x³e^－x，

即

特解为

常系数线性微分方程组的解法

(1)齐次方程组

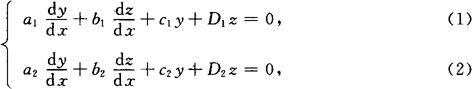
其中a_i，b_i，c_i，D_i(i=1，2)均为常数．

由(1)，(2)解出(它们均由y，z表示)，记为

由(3)解出z代入(4)，得到关于y的二阶常系数齐次方程，从而解得y，再代入(3)而得z．

(2)非齐次方程组

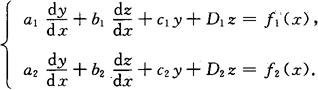
仿齐次方程组的解法．