分块矩阵
书籍:数学手册(大学生用)
出处:按学科分类—数理科学和化学 清华大学出版社《数学手册(大学生用)》第289页(1191字)
分块矩阵
设A是m×n矩阵,在行的方向分成s块,列的方向分成t块,则称A为s×t分块矩阵,记作Am×n=(Akl)s×t,其中Akl(k=1,2,…,s;l=1,2,…,t)称为A的子块.
常用分块法
1.按行分块
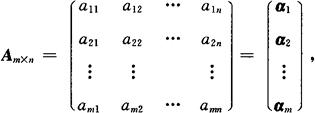
其中αi=(ai1,ai2,…,ain)(i=1,2,…,m).
2.按列分块
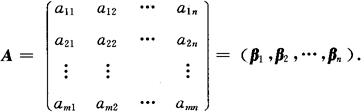
其中βj=(a1j,a2j,…,amj)T(j=1,2,…,n).
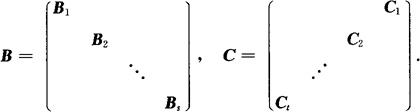
3.准对角矩阵(对角块矩阵)
4.2×2矩阵
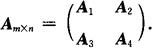
分块矩阵的运算
1.分块矩阵的加法
设A,B是同型矩阵,且分块方法一致,有
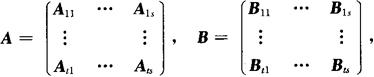
则
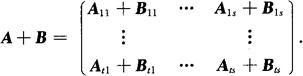
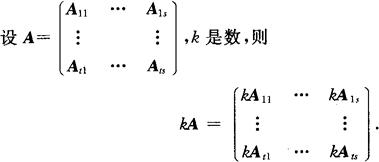
2.数与分块矩阵的乘法
3.分块阵的乘法
设A是m×s矩阵,B是s×n矩阵,且A的列的分法与B的行的分法一致,即

其中Ai1,Ai2,…,Ail的列数分别与B1j,B2j,…,Blj的行数相等,则

其中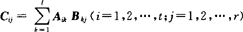 .
.
4.分块矩阵的转置
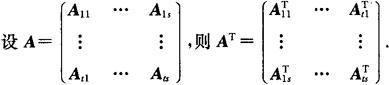
5.分块矩阵的逆

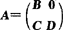 ,其中B,D可逆,则A可逆,且
,其中B,D可逆,则A可逆,且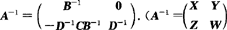 ,利用定义,可求得X,Y,Z,W,从而求得A-1.)
,利用定义,可求得X,Y,Z,W,从而求得A-1.) 6.分块矩阵的行列式
设A是n阶矩阵,B是m阶矩阵,则
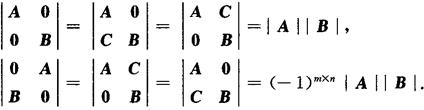
当m=n时,因n2和n有相同的奇偶性,故
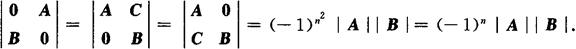
上一篇:克拉默法则
下一篇:数学手册(大学生用)目录