齐次线性方程组

出处：按学科分类—数理科学和化学 清华大学出版社《数学手册（大学生用）》第316页（1995字）

齐次线性方程组的表示形式

(1)一般形式

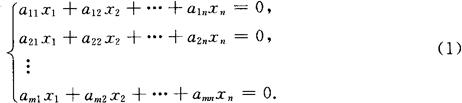
n是未知量个数，m是方程个数，a_ij是第i个方程的第j未知量x_j的系数．

(2)向量形式

α₁x₁+α₂x₂+…+α_nx_n=0，

其中，j=1，2，…，n．

(3)矩阵形式

A_m×nx=0

其中

A是称为方程组(1)的系数矩阵．

有解条件

A_m×nx=0必有解，至少有零解；

A_m×nx=0，当n＞m时，有非零解；

A_n×nx=0有非零解(只有零解)的充分必要条件是|A|=0(|A|≠0)；

A_m×n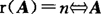，的列向量组线性无关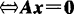惟一零解；

A_m×n，的列向量组线性相关有非零解，且有无穷多解，其中线性无关解向量个数为n一r个．

解的性质 若ξ₁，ξ₂是方程组(1)的解，则kξ₁，ξ₁+ξ₂，k₁ξ₁+k₂ξ₂也是方程组(1)的解．

基础解系 若ξ₁，ξ₂，…，ξ_n－r是A_m×nx=0的解，且满足(1)ξ₁，ξ₂，…，ξ_n－r线性无关，(2)任何Ax=0的解向量ξ均可由ξ₁，ξ₂，…，ξ_n－r线性表示，则称向量组ξ₁，ξ₂，…，ξ_n－r是Ax=0的基础解系．

ξ₁，ξ₂，…，ξ_n－r是Ax=0的基础解系的充要条件是ξ₁，ξ₂，…，ξ_n－r是Ax=0的线性无关解，其中r(A)=r，n是Ax=0的未知量的个数．

解的结构 Ax=0的通解为

k₁ξ₁+k₂ξ₂+…+k_n－rξ_n－r，

其中ξ₁，ξ₂，…，ξ_n－r是Ax=0的基础解系，k₁，k₂，…，k_n－r是任意常数．

方程组的初等变换

(1)用一个非零常数k乘一个方程；

(2)把一个方程乘c后加到另一个方程；

(3)互换两个方程的位置；

以上三种变换称为方程组的初等变换．

同解方程组 如果两个方程组有相同的解集合，则称这两个方程组是同解方程组．

求解方法，高斯消元法 初等变换将方程组变成与它同解的方程组．

方程组做初等变换，等价于其对应系数矩阵做初等行变换，且一定可以通过一系列初等行变换化成阶梯形矩阵．设A_m×n，r(A)=r，不妨设A的前r列线性无关．

全零行表示多余方程，m－r行非零行是独立方程(r个)．x₁，x₂，…，x_r称独立未知量，x_r+1，…，x_n称自由未知量．

求解阶梯形矩阵对应的方程组

解法1：令x_r+1=k₁，x_r+2=k₂，…，x_n=k_n－r，回代入阶梯形方程组依次求出xr，xr－1，…，x1，得通解

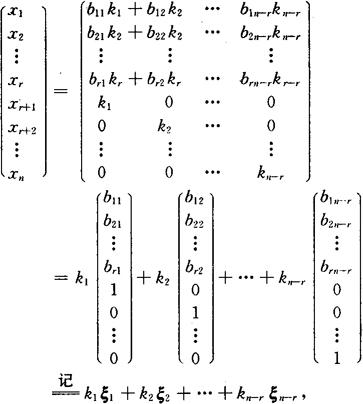
其中ξ₁，ξ₂，…，ξ_n－r是Ax=0的基础解系．

解法2：自由未知量(x_r+1，x_r+2，…，x_n)分别赋值(1，0，…，0)，(0，1，…，0)，…，(0，0，…，1)，回代入阶梯形方程组分别求得n－r个解向量．

则ξ₁，ξ₂，…，ξ_n－r是Ax=0的基础解系，方程组的通解为

k₁ξ₁+k₂ξ₂+…+k_n－rξ_n－r，

其中k₁．k₂．…，k_n－r是任意常数．