线性变换

出处：按学科分类—数理科学和化学 清华大学出版社《数学手册（大学生用）》第350页（2551字）

线性变换的定义 数域F上的n维线性空间S_n内自身到自身的映射σ称为S_n上的一个变换，若S_n内的变换σ满足条件：

(1)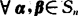，有σ(α+β)=σ(α)+σ(β)；

(2)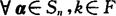，有σ(kα)=kσ(α)，

则称σ为S_n的一个线性变换．

线性变换的性质

(1)σ(0)=0；

(2)σ(－α)=－σ(α)；

(3)线性相关向量组经过线性变换后它们的像向量组仍保持线性相关．

注 逆命题不成立，即线性无关向量组经过线性变换后，其像向量组可能变换成线性相关．

一个线性变换σ由它在一组基上的作用惟一确定．

若ε₁，ε₂，…，ε_n是线性空间S_n的一组基，α₁，α₂，…，α_n是S_n中的任意n个向量，则有惟一的一个线性变换σ，使得

σ(ε_i)=α_i，i=1，2，…，n．

线性变换的相等 若σ和τ是Sn上的两个线性变换，ε₁，ε₂，…，ε_n是S_n的一组基．若

σ(ε_i)=τ(ε_i)，i=1，2，…，n，

则有 σ=τ．

线性变换在一组基下的对应矩阵设ε₁，ε₂，…，ε_n是线性空间S_n的一组基，σ是S_n的一个线性变换，σ(ε_i)(i=1，2，…，n)可以惟一的由ε₁，ε₂，…，ε_n线性表示，记为

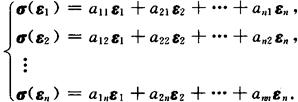
即

σ(ε₁，ε₂，…，ε_n)=(σ(ε₁)，σ(ε₂)，…，σ(ε_n))

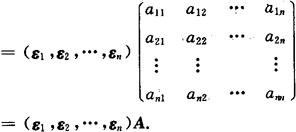
矩阵

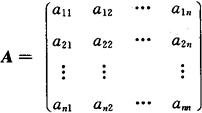
称为线性变换σ在基ε₁，ε₂，…，ε_n下的对应矩阵，其中A中第j列是σ(ε_j)在基ε₁，ε₂，…，ε_n下的坐标．

像向量的坐标 设σ是n维线性空间S_n的线性变换，ε₁，ε₂，…，ε_n是S_n的一组基，S_n中向量α在基下的坐标为(x₁，x₂，…，x_n)，则像向量σ(α)在基ε₁，ε_2，…，ε_n的坐标为(y₁，y₂，…，y_n)，且

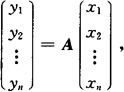
其中A是σ的对应矩阵．

同一个线性变换在不同基下的对应矩阵是相似矩阵

若σ在基ξ₁，ξ₂，…，ξ_n下的对应矩阵是A，在基η₁，η₂，…，η_n下的对应矩阵是B，而ξ₁，ξ₂，…，ξ_n到η₁，η₂，…，η_n的过渡矩阵是C，则

B=C^－1AC．

相似矩阵可看做同一个线性变换在不同基下的对应矩阵．

线性变换的运算 设σ，τ是线性空间S_n的两个线性变换，则定义

加法：(σ+τ)(α)=σ(α)+τ(α)；

数乘：(kσ)(α)=kσ(α)；

乘法：(τσ)(α)=τ(σ(α))．

且σ+τ，kσ，τσ仍是线性变换．若σ，τ在S_n的基ε₁，ε₂，…，ε_n下的对应矩阵是A，B，则σ+τ，kσ，τσ在基ε₁，ε₂，…，ε_n的对应矩阵分别是A+B_，kA，BA．

线性变换的特征值和特征向量 设σ是线性空间S_n的线性变换，α是S_n上的一个非零向量，若

σ(α)=λ₀α，

其中λ₀是S_n中的数域F上的常数，则称λ₀是σ的特征值，α是σ的属于特征值λ₀的特征向量．

σ与其对应矩阵A的特征值、特征向量的关系

设σ在S_n中基ε₁，ε₂，…，ε_n下的对应矩阵是A，σ的特征向量α在该基下的坐标为x=(x₁，x₂，…，x_n)，那么，若σ(α)=λ₀α，则有Ax=λ₀x．

线性变换的值域和核 设σ是线性空间S_n的一个线性变换，则由σ的全体像组成的集合称为σ的值域，记作Imσ，即

Imσ=｛σ(α)|α∈S_n｝．

Imσ是S_n的子空间，它的维数称为σ的秩，记作r(σ)，即r(σ)=dim(Imσ)．

线性变换的核 由所有被σ变成零向量的向量组成的集合称为σ的核，记作Kerσ，即

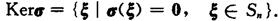
Kerσ也是S_n的子空间，Kerσ的维度称为σ的零度，记作n(σ)，即n(σ)=dim(Kerσ)．

有关线性变换值域与核的性质

若ε₁，ε₂，…，ε_n是S_n的一组基，A是σ在这组基下的对应矩阵，则

(1)Imσ=L(σ(ε₁)，σ(ε₂)，…，σ(ε_n))．

(2)r(σ)=r(A)．

(3)dim(Kerσ)+dim(Imσ)=n=dimS_n=r(σ)+n(σ)．