条件概率
出处:按学科分类—数理科学和化学 清华大学出版社《数学手册(大学生用)》第370页(1595字)
条件概率的定义 设两事件A,B,且P(A)>0,则称

为事件A发生的条件下,事件B发生的条件概率.
条件概率与概率有相同的性质:
(1)对任一事件B,0≤P(B|A)≤1;
(2)P(Ω|A)=1;
(3)若B1,B2,…是两两互斥事件,则有

(4)对任意两事件B1,B2,有
P(B1∪B2|A)=P(B1|A)+P(B2|A)-P(B1B2|A).
条件概率中的条件事件A起着样本空间的作用,被称为缩小的样本空间.
乘法定理(公式) 对事件A,B,且P(A)>0,P(B)>0,则有
P(AB)=P(A)P(B|A),
P(AB)=P(B)P(A|B);
推广:对事件A1,A2,…,An,且P(A1A2…An-1)>0,则有
P(A1A2…An)=P(A1)P(A2|A1)…P(An|A1A2…An-1).
乘法公式是计算交事件概率的基本公式.
全概率公式和逆概率公式
1.全概率公式
(1)划分(分割):设Ω为随机试验E的样本空间,B1,B2,…,Bn为E中的一组事件,如果① ,i,j=1,2,…,n.②
,i,j=1,2,…,n.② .则称{B1,B2,…,Bn}为样本空间Ω的一个划分(又叫分割,分划).
.则称{B1,B2,…,Bn}为样本空间Ω的一个划分(又叫分割,分划).
若{B1,B2,…,Bn}为Ω的一个划分,则对每次试验,事件B1,B2,…,Bn中必有一个且仅有一个发生.
(2)全概率公式:设Ω是试验E的样本空间,A为E中的一个事件.{B1,B2,…,Bn}为Ω的一个划分,且P(Bi)>0(i=1,2,…,n),则有
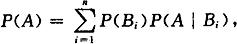
并称之为全概率公式.
概率论的重要问题之一就是希望从已知的比较简单的事件的概率,推算出未知的比较复杂的事件的概率.为此,人们在处理问题时,经常把一个复杂事件分解成若干个互斥的简单事件的并,再分别计算这些简单事件的概率,最后利用概率的可加性,得出复杂事件的概率.全概率公式就是起着这种重要作用的基本公式.它在实践中有着广泛的应用.
2.逆概率公式(贝叶斯公式)
通常称概率P(Bi|A)为P(A|Bi)的逆概率,自然就称计算概率P(Bi|A)的公式为逆概率公式.
设Ω是试验E的样本空间,A为E中的一个事件,{B1,B2,…,Bn}为Ω的一个划分,且P(A)>0,P(Bi)>0(i=1,2,…,n),则有

这就是逆概率公式(贝叶斯公式).