欧氏空间
出处：按学科分类—数理科学和化学 清华大学出版社《数学手册（大学生用）》第355页（1769字）
内积 设V是实数域上的线性空间，如果对V内的每一对向量α，β，都与一个确定的实数对应，这个实数记为(α，β)，并且满足下列条件：
(1)对称性：(α，β)=(β，α)；
(2)线性性：(α+β，γ)=(α，γ)+(β，γ)，(kα，β)=k(α，β)；
(3)正定性：(α，α)≥0，等号成立当且仅当α=0，则称这个实数(α，β)为向量α，β的内积，又称数量积或点积．
欧氏空间
定义了内积的实数域上的线性空间称为欧氏空间．即有了向量的度量性质的线性空间称为欧氏空间．
向量的长度
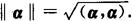
两向量间的夹角的余弦
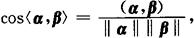
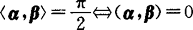，此时称两向量α，β正交．
柯西不等式
|(α，β)|≤‖α‖‖β‖．
三角不等式
‖α+β‖≤‖α‖+‖β‖．
度量矩阵 设ε1，ε2，…，εn是Vn的一组基，且有(εi，εj)=aij(i，j=1，2，…，n)(显然aij=(εi，εj)=(εj，εi)=aji，i，j=1，2，…，n)，令
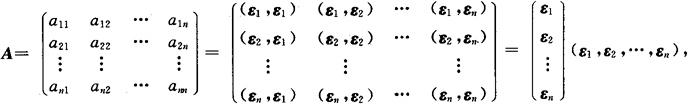
其中A=AT，(元素的乘法是内积)则称A是Vn在基ε1，ε2，…，εn下的度量矩阵．显然度量矩阵由Vn的一组基的内积所确定．
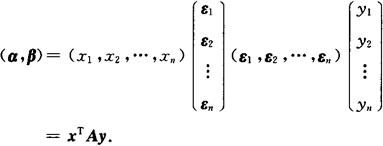
内积的坐标表达式 设ε1，ε2，…，εn是Vn的一组基，α=x1ε1+x2ε2+…+xnεn，β=y1ε1+y2ε2+…+ynεn，则
不同基下的度量矩阵是合同矩阵 设ε1，ε2，…，εn；η1，η2，…，ηn是Vn的两组基，其中
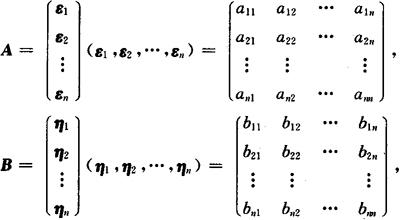
且(η1，η2，…，ηn)=(ε1，ε2，…，εn)C，则有B=CTAC．
标准正交基 若ε1，ε2，…，εn是欧氏空间的一组基，且满足
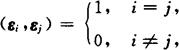
则称基ε1，ε2，…，εn为标准正交基．
标准正交基下的度量矩阵是单位矩阵 W是欧氏空间V的一个子空间，α是V的一个向量，若对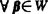
，都有
(α，β)=0，
则称α与W正交，记作α⊥W．
正交子空间 设W1，W2是欧氏空间的两个子空间，若对于
W2，都有
(α，β)=0，
则称W1，W2正交，记作W1⊥W2．
正交补W1，W2是欧氏空间V的两个子空间，满足
W1⊥W2，W1+W2=V，
则称W2为W1的正交补(或W1是W2的正交补)．正交补是惟一的，记作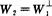
．
正交变换 如果欧氏空间的线性变换σ保持向量的内积不变，即对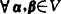
，有
(σ(α)，σ(β))=(α，β)，
则称σ是正交变换．
正交变换的充分必要条件 σ是V的正交变换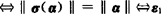
，ε2，…，εn是标准正交基，则σ(ε1)，σ(ε2)，…，σ(εn)也是标准正交基
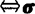在标准正交基下的对应矩阵是正交矩阵．