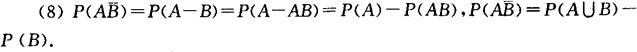随机事件的概率

出处：按学科分类—数理科学和化学 清华大学出版社《数学手册（大学生用）》第366页（1620字）

随机事件的概率的定义 对一个随机事件A，如果用一个数能表示事件A发生的可能性的大小，则称这个数为事件A的概率，记作P(A)．简言之，事件A的概率就是事件A发生的可能性大小的数量描述．

古典概型的特点

(1)样本空间由有限个样本点构成Ω=｛e₁，e₂，…，e_n｝；

(2)每个样本点出现的可能性相等：．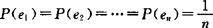

古典概型事件A的概率计算公式

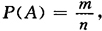
其中n为样本空间中样本点总数，m为事件A包含的样本点个数．

概率的统计定义

1．频率

设在随机试验E中进行n次重复试验．如果事件A出现n_A次，则比值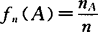称为事件A出现的频率．

频率的一般性质：

(1)0≤f_n(A)≤1；

(2)f_n(Ω)=1；

(3)若事件A₁，A₂互斥，则f_n(A₁∪A₂)=f_n(A₁)+f_n(A₂)．

推广：若事件A₁，A₂，…，A_k两两互斥，则

2．概率的统计定义

在随机试验E中，当试验次数n逐渐增大时，频率值f_n(A)趋于稳定，即在某个数p附近波动，称数p为事件A的概率，即P(A)=p．当n很大时，f_n(A)≈p．人们总是用n很大时的f_n(A)作为P(A)的近似值，即P(A)≈f_n(A)(n很大)．

概率的公理化定义 设有随机试验E，样本空间为Ω，对于E中的事件A，赋予一个实数P(A)，如果满足

(1)0≤P(A)≤1；

(2)P(Ω)=1；

(3)对任何两两互斥的事件组｛A_i｝(i=1，2，3，…)有

则称P(A)为事件A的概率．

概率的性质

(1)对任何事件A都有0≤P(A)≤1；

(2)P(Ω)=1，；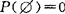

(3)对两两互斥事件组有；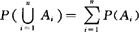

(4)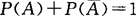，或，；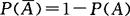

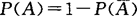(5)加法定理：对任何事件A，B，有

P(A∪B)=P(A)+P(B)－P(AB)；

推广：设有n个事件，A₁，A₂，…，A_n，则有

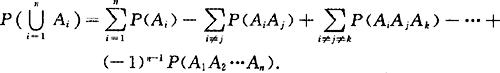
(6)：

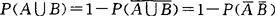推广：．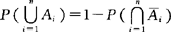

(7)若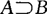，则P(A－B)=P(A)－P(B)，并且P(A)≥P(B)；