抽样分布

出处：按学科分类—数理科学和化学 清华大学出版社《数学手册（大学生用）》第426页（2650字）

统计量的分布叫抽样分布．

分位点(又叫分位数) 设有统计量U服从某分布，如果P｛U＞u_α｝=α(0＜α＜1)，则称u_α为该分布的上α分位点．分位点都可在专门的数表上查出．

标准正态分布 U～N(0，1)，密度函数

它的分位点记为zα(见图6．1)．

图6．1

P｛U＞z_α｝=α，P｛U≤z_α｝=Φ(z_α)=1－α，反查表查出z_α．

X²分布

1．定义

设总体X～N(0，1)，X₁，X₂，…，X_n为简单随机样本(Xi～N(0，1))，统计量X²为

则称X²所服从的分布为自由度是n的X²分布，记为X²～X²(n)．

它的概率密度函数为

图形如图6．2．

图6．2

X²(1)分布是Γ分布．

X²(2)分布是指数分布．

2．X²(n)分布表

对给定的α(0＜α＜1)，若有一点，如果，

则称此点为X²(n)分布的上α分位点(见图6．2)．

3．X²(n)分布的可加性

若，，且相互独立，则．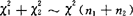

4．X²(n)的期望和方差

E(X²(n))=n，D(X²(n))=2n．

t分布

1．定义

设U～N(0，1)，V～X²(n)，U，V相互独立，记

则称T所服从的分布为自由度是n的t分布．记为T～t(n)．它的概率密度函数为

图形如图6．3．

图6．3

f(t)是偶函数，图形对称于中心轴t=0．

2．t(n)分布表

对给定的α(0＜α＜1)，若有一点t_α(n)，如果满足

P｛T＞t_α(n)｝=α，

则称此点为t(n)分布的上α分位点(见图6．3)．

3．t_1－α(n)=－t_α(n)．

4．，即t(n)分布的极限分布为N(0，1)分布．

当n很大时，t(n)分布近似为N(0，1)分布．当n≥50时，t_α(n)≈z_α，这里z_α为标准正态分布的上α分位点．

F分布

1．定义

设U～X²(n₁)，V～X²(n₂)，U，V相互独立．记

则称F所服从的分布为F(n₁，n₂)分布，自由度为(n₁，n₂)．

它的概率密度函数为

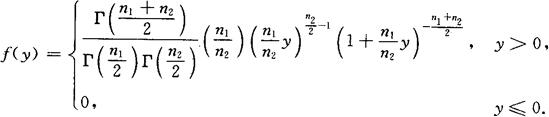
f(y)的图形如图6．4所示．

图6．4

2．F(n₁，n₂)分布表

对给定的α(0＜α＜1)，若有一点F_α(n₁，n₂)，如果满足

P｛F＞F_α(n₁，n₂)｝=α，

则称F_α(n₁，n₂)为F(n₁，n₂)分布的上α分位点(见图6．4)．

3．性质

常用统计量的分布

1．一个正态总体

设X～N(μ，σ²)，X₁，X₂，…，X_n为简单随机样本，则有

2．两个正态总体

设X～N(μ₁，)，Y～N(μ₂，)，X，Y相互独立，它们的简单随机样本分别为X₁，X₂，…，X_n1；Y₁，Y₂，…，Y_n2，，，则有

(2)若，

(3)若

记，称之为复合样本方差．称为复合标准差，