试验数据处理

出处：按学科分类—工业技术 北京理工大学出版社《新编液压工程手册下册》第2107页（2007字）

对于任何试验来说都要通过各种试验方法和测试手段来获取试验数据。但这些原始数据并不是我们所要求的结果，还必须对它们进行处理后才能达到预定的目的。从试验的整个过程来看，对试验数据的处理是一个很重要的环节。只有在处理的基础上才能得到各种特性曲线和性能指标，作出合理的试验结论。

数据处理的方法很多，过去往往是人工手记、手算、列表、画曲线、求方程等。现代发展为试验数据数字显示、打印输出、记录仪自动记录和存贮、自动描绘特性曲线、数据处理系统自动分析和处理数据。以计算机为中心的实时分析处理系统同时还参与试验过程的控制(即CAT)。

常用的试验数据表示方法有：

(1)试验数据列表法

列表法就是将测得的数据，按照自变量的变化顺序，对应列出各因变量随它而变化的数值。列表法具有的优点如下：方法简单、形式紧凑、数据表示清楚明了，互相之间进行比较很方便；在同一表格内可同时表示很多变量之间的相互关系而不混乱。

(2)试验数据的图形表示法

通过采用各种坐标系，如直角坐标、极坐标、对数坐标、立体三维坐标系等，将试验数据以曲线、曲面、体积等图形表示出来就是图形表示法。在数据处理中此方法应用极为普遍。通过图形可以弥补试验点的不足，直接找到中间的过渡值而不需要另作插入计算。另外从图形上可直接微分，即求曲线上某点的切线斜率；还可对自变量求积分，即求曲线下某区段内的面积等。还可以根据图形的形状，按数学方法拟合曲线的方程，找到参数之间的函数关系或经验公式。

根据试验数据作图时应注意的事项有：

A．图纸的选择

根据试验数据和试验目的，确定应采用的坐标形式后，就可选择坐标纸。常用的坐标纸有：直角坐标纸，俗称方格纸；对数坐标纸，它又分为单对数和双对数坐标纸；还可按需要选不同数量的十倍频程的坐标纸。另外还有极坐标纸。

B．坐标的分度原则

习惯上以横坐标(x轴)代表自变量，纵轴(y轴)代表因变量。所谓分度就是沿坐标轴以一定的长度间距代表一定数值大小来划分刻度的工作。分度时总的原则就是要使每一试验点的数据值能迅速而方便地在坐标轴上找到。一般分度间距为1、2、4、5等较为方便。

因为直线是最容易画的，且画的时候误差也最小。所以在进行数据处理时，通过坐标轴按不同的函数规律分度，使参数之间的关系变为线性关系或近于线性关系。例如若自变量t与因变量P之间的函数关系为

P=Ctⁿ

C和n均为常数，此式为指数关系。若将此函数式稍加变换，等式两边都取对数，则得到

1ogP=logC+nlogt

可见变成了直线方程。采用双对数直角坐标，则在此坐标平面上画出为一直线，如图35．1－12所示。1ogC为截距，n为直线的斜率n=tga。

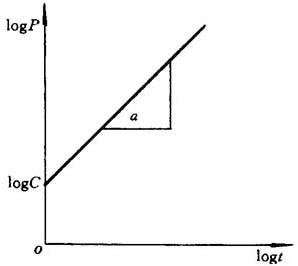
图35．1－12 曲线－直线变换图

当然，如果函数关系比较复杂时，要变成线性关系并不容易。对于直角坐标，一般常用的关系有：x－y、logx－y、logx－logy、xⁿ－y、x^1／n－y、x－(1／y)、(1／x)－y等。

C描点和逐点描迹作曲线的方法

描点就是根据试验数据，由坐标轴上的点找出坐标平面上的点［(x，y)或(R，θ)］的位置来。以直角坐标为例，由于在x轴上自变量的点与y轴上因变量的点都带有误差，因而坐标平面上的点(x，y)就不能用简单的点来表示，而要用一矩形来表示，如图35．1－13所示。矩形的边的长度分别代表自变量或因变量的误差大小，矩形的中心就是算术平均值。若两变量的误差大小相等，则可把矩形改为圆，半径代表误差大小。若要在同一坐标平面上画出几个因变量随同一自变量的变化曲线时，对应每一个因变量的数据点必须用不同的符号表示，也可用不同颜色来区别。总之必须能表示清楚，使人一目了然。

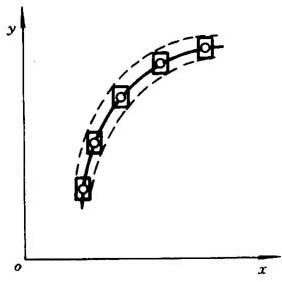
图35．1－13 具有误差的数据点的曲线图