图解复数法作平面机构的运动分析
出处:按学科分类—工业技术 北京出版社《现代综合机械设计手册中》第1893页(8092字)
分析的方法与步骤是:首先作位置分析,画出机构的位置矢量图,由图写出复数形式的位置矢量方程,解方程求未知的位置参数;其次作速度、加速度分析,将一般形式的速度、加速度矢量方程变成复数形式,解复数方程求速度、加速度。
如图5.3-1所示,矢量R可用带箭头的线段表示,也可用复数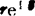 表示,即
表示,即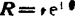 ,其中v为矢量R的大小;θ为矢量R的方位角,
,其中v为矢量R的大小;θ为矢量R的方位角,
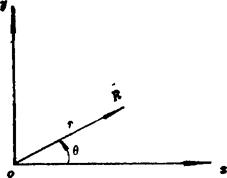
图5.3-1 矢量与复数
度量矢量方位角的起始线是由矢量起点向右引出的水平线:由起始线按逆时针方向度量的方位角取“+”值;由起始线按顺时针方向度量的方位角取“-”值。显然, 。当r=1时,
。当r=1时,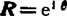 (
(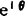 为单位矢量)。图5.3-2所示为
为单位矢量)。图5.3-2所示为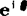 圆。可见:
圆。可见:
 ;
;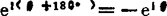 ;
;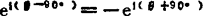 。
。
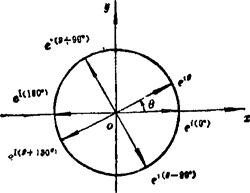
图5.3-2 eiθ圆
在图5.3-3中,a)所示为一平面运动构件。b)表示构件的C点对B点的相对位置矢量BC,即BC=le1φ(l为B至C的实际长度)。通常规定:角速度ω为逆时针方向时取“+”值,反之取“-”值;角加速度ε为逆时针方向时取“+”值,反之取“-”值。当ω为“+”值时,vcB的方位角为φ+90°,如图c)所示;当ω为“-”值时,vCB的方位角为φ-90°。
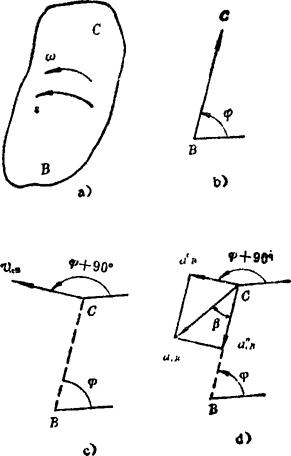
图5.3-3
由于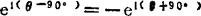 ,故vCB=lωe1(φ+90)。同理,
,故vCB=lωe1(φ+90)。同理,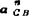 =
=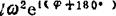 =
=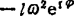 :
: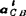 =
=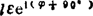 ;
;
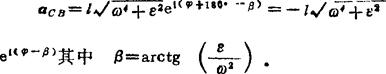
用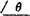 代替
代替 表示一矢量的具体结果则更为简明。如vCB的大小为10m/s,方位角为-60°时,可表示为:
表示一矢量的具体结果则更为简明。如vCB的大小为10m/s,方位角为-60°时,可表示为: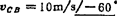 。
。
如图5.3-4中a)所示,导杆1作平面运动,滑块2沿导杆1作往复直线移动,B点为两构件的瞬时重合点,动坐标系与导杆1固结。
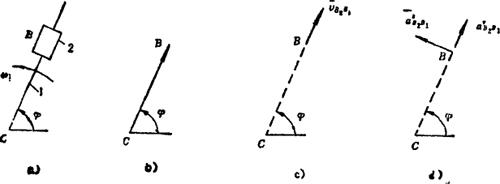
图5.3-4
相对速度vB2B1的复数形式:因vB2B1的方位角为φ或为φ+180°。且vB2B1往往是待求量,故可假设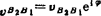 。若求得vB2B1=10m/s,则vB2B1=
。若求得vB2B1=10m/s,则vB2B1=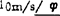 ;若vB2B1=-10m/s,则vB2B1=10m/s
;若vB2B1=-10m/s,则vB2B1=10m/s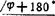 。
。
哥氏加速度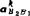 的复数形式:因vB2B1=vB2B1e1φ,故
的复数形式:因vB2B1=vB2B1e1φ,故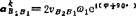 。若计算得vB2B1ω1=-5m/s2,显然,
。若计算得vB2B1ω1=-5m/s2,显然,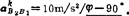
相对加速度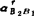 的复数形式:可假设
的复数形式:可假设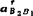 =
=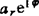
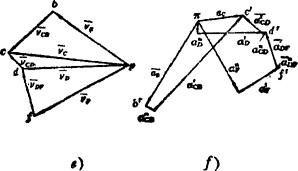
例5.3-15曲柄滑块机构,见图a)。已知l1=20mm、l2=60mm、φ1=60°、ω1=10rad/s),求φ2、S、ω2、vC、ε2、aC。
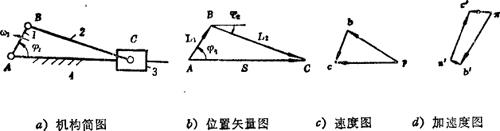
位置分析:
画出位置矢量图(见图b),由图可写出复数形式的位置矢量方程
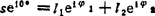 (A)
(A)
(A)式取虚部 0=l1sinφ1+l2sinφ2
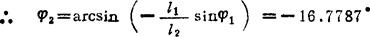
(φ2为负值表示由起始线按顺时针度量的值,如图示)
(A)式取实部 S=l1cosφ1+l2rosφ2
=67.4456mm。
速度分析:
考虑构件2的B、C两点,可写出一般形式的速度矢量方程
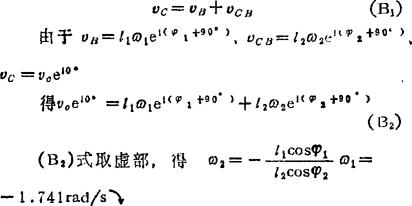
(B2)式取实部,得 vC=-(l1ω1sinφ1+l2ω2sinφ2)=-0.203m/s
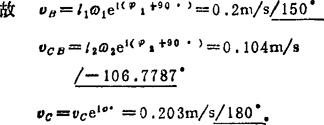
由(B1)式可画出速度图(见图c示意图)。
加速度分析:
考虑构件2的B、C两点,可写出一般形式的加速度矢量方程

例5.3-16 正切机构,如图a)所示。已知H=30mm、φ1=30°、ω1=10rad/s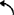 ,求v3、a3。
,求v3、a3。
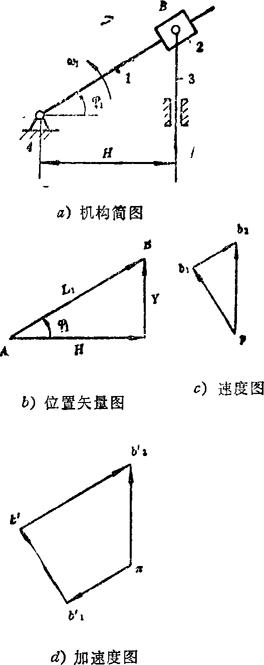
画位置矢量图(见图b),由图写出位置矢量方程
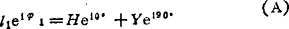
由(A)式取实部,得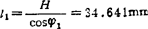
由图得 Y=Htgφ1=17.321mm
速度分析:
考虑构件1、2的重合点(B1、B2),可写出速度矢量方程
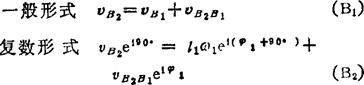
由(B2)式取实部,得vB2B1=/1ω1tgφ1=0.2m/s
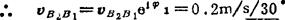
由(B2)式取虚部,得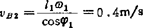
∴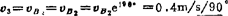
由(B1)式可画出速度图(见图c)。
加速度分析:
考虑构件1、2的重合点(B1、B2),可写出加速度矢量方程;
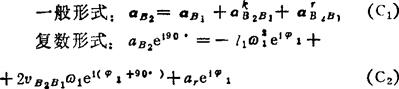
用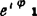 除(C2)式两边:
除(C2)式两边: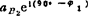 =-
=-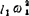 +2vR2B1ω1e190°+ar
+2vR2B1ω1e190°+ar
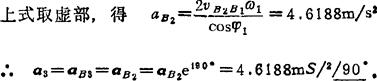
由(C1)式可画出加速度图(见图d).
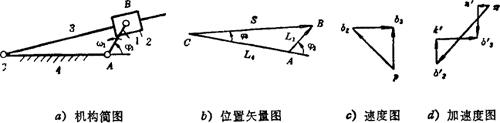
例5.3-17 导杆机构,如图a)所示。已知l1=20mm、l4=50mm、φ1=60°、ω1=10rad/s,求ω2,ε3。
位置分析:
画出位置矢量图b),由图可写出位置矢量方程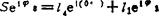 (A)
(A)
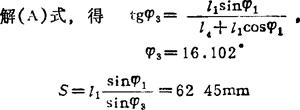
速度分析:
速度矢量方程 vB3=vB2+vB3B2 (B1)
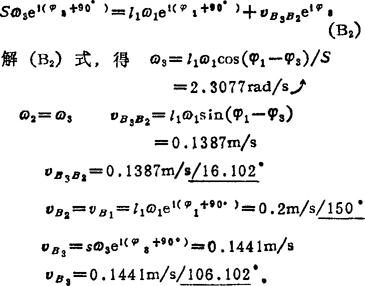
加速度分析:
由(B1)式可画出速度图(见图c)。
加速度矢量方程
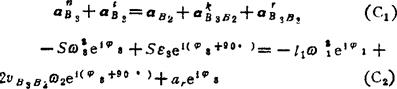
用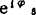 除(C2)式两边后,取虚部,得
除(C2)式两边后,取虚部,得
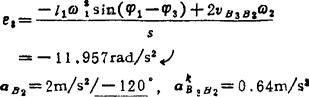
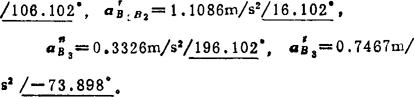
由(C1)式可画出加速度图。
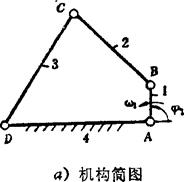
例5.3-18 铰链四杆机构。如图a)所示,已知l1=20mm、l2=60rnm、l3=70mm、l4=80mm,φ1=90°、ω1=10rad/s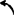 ,求φ2、φ8、ω2、ω3、ε2、ε2、
,求φ2、φ8、ω2、ω3、ε2、ε2、 、
、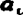 。
。
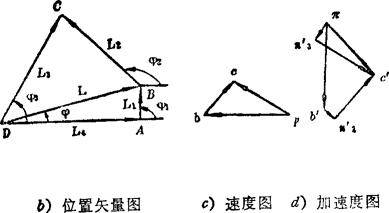
位置分析:
画位置矢量图(见图b),由图得
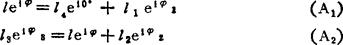
由(A1)式解得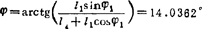
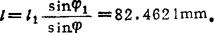
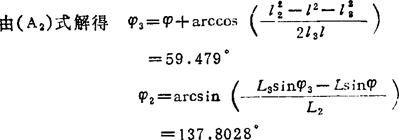
速度分析:
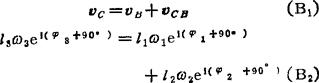

由(B1)式可画出速度图(见图c示意图)。
加速度分析:
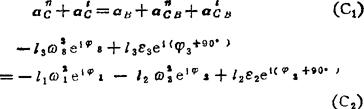
由(C2)式解得:
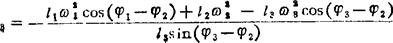

其中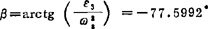 。
。
由(C1)式可画出加速度用(见图d示意图)。
例5.3-19 曲柄摇块机构,如图a)所示,已知l1=30mm、l4=100mm、φ1=135°、ω1=10rad/s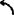 ,求ω1、ε1。
,求ω1、ε1。
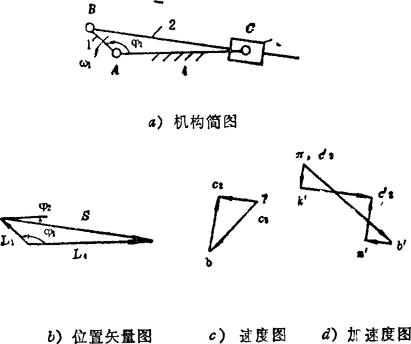
位置分析:
画出位置矢量图(见图b),由图可写出复数形式的位置矢量方程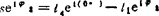 (A)
(A)
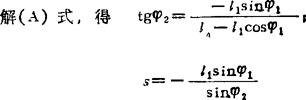
φ2=-9.9267°;s=123.0554mm速度分析:

因此复数形式的速度矢量方程为
vc2c3e1φ2=l1ω1e1(φ1+90°)+Sω2e1(p2+90°)
(B2)
解(B2)式,得vc2c3=-l1ω1sin(φ1-φ2);
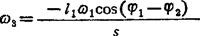
结果:vc2c3=-0.1724m/s即vc2=vc2co=0.1724m/s/170.0733。ω2=1.9952rads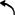 ;ω3=ω2=1.9952rad/s
;ω3=ω2=1.9952rad/s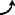 ;vB=l1ω1e1(
;vB=l1ω1e1(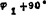 )=0.3m/s/225°;vc2B=Sω2e1(φ2+90°)=0.2455m
)=0.3m/s/225°;vc2B=Sω2e1(φ2+90°)=0.2455m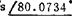 可按(B1)式画出速度图(见图c)。
可按(B1)式画出速度图(见图c)。
加速度分析:
一般形式的加速度矢量方程
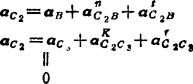
由上两式联立,得
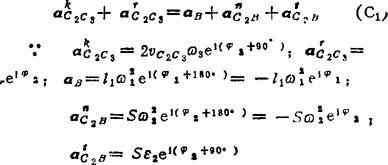
因此复数形式的加速度矢量方程为
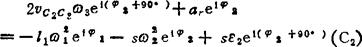
用e1φ2除(C2)式两边,得
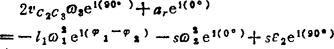
上式取虚部,得
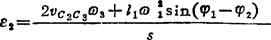
上式取实部,得 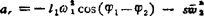
结果:ε2=8.4188rad/s2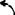 :
: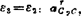 =1.9654m/s2/-9.9267°。
=1.9654m/s2/-9.9267°。
由(C1) 式可画出加速度图(见图d)。
例5.3-20 四杆机构,如图a)所示,已知l2=25mm、l3=10mm、l4=40mm、φ1=60°、ω1=10rad/s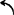 ,求ω3、ε3。
,求ω3、ε3。
位置分析:
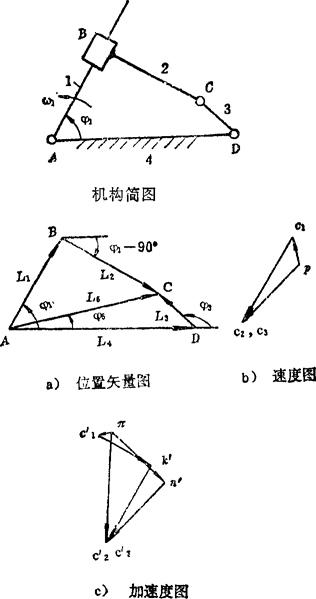
画出位置矢量图(见图b)由图可写出复数形式的位置矢量方程
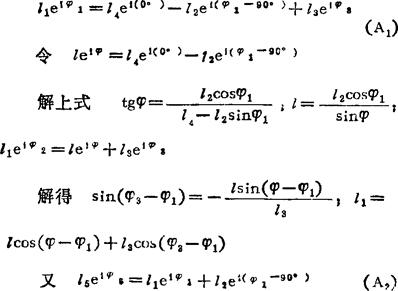
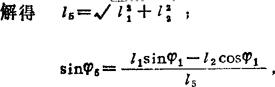
结果 φ=34.2636°7l=22.2025mm;φ3=134.6013°,l1=22.6553mm;φ5=12.1833°:l5=33.7381mm。
速度分析:
由构件1、2的重合点(C1、C2)写出一般形式的速度矢量方程
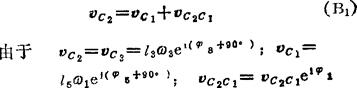
故可写出复数形式的速度矢量方程
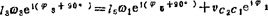 (B2)
(B2)
解(B2)式,得 ;vc2c1=l5ω1sin(φ5-φ1)-l3ω3sin(φ3-φ1)
;vc2c1=l5ω1sin(φ5-φ1)-l3ω3sin(φ3-φ1)
结果;ω3=85.3211rad/s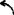 :vc2c1=-1.0726m/s。
:vc2c1=-1.0726m/s。
由(B1)式可画出速度图(见图c)。
加速度分析:
一般形式和复数形式的加速度矢量方程分别为
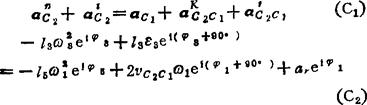
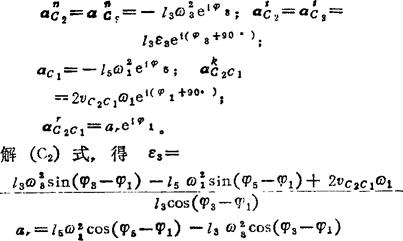

例5.3-21 六杆机构,如图a)所示,此六杆机构有1个三副构件(CDF),经3个二副构件(CB、DE、FG)连于原动件及机架(BAEG),属Ⅲ级机构。
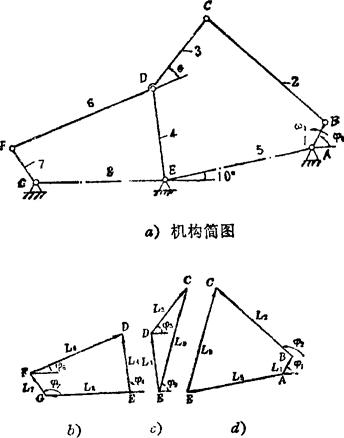
已知l1=10mm、l2=53mm、l3=30mm、l4=30mm、l5=50mm、l6=51mm、l7=14mm、l =44mm、θ=30°、ω1=10rad/s
=44mm、θ=30°、ω1=10rad/s ,
,
求φ1=60°时的ω2、ω3、ω4、ω7,ε2、ε3、ε4、ε7。
位置分析:
由机构简图可画出图b)、c)、d)所示的位置矢量图,由图可写出如下的复数形式的位置矢量方程
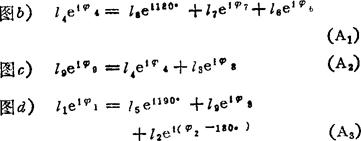
求φ1=60°时的φ2、φ3、φ6、φ4、φ7,可用牛顿迭代法,即初给-φ7,按(A1)、(A2)、(A3)式的顺序求得φ1,并计算y1=ω1/ω7,Y=φ1-60若Y<0.0001(指定的精度要求),则认为所给的φ7及算出的φ2、φ3、φ4、φ6即为与φ1=60°对应的值;否则,应将原来的φ7减去Y/Y1后所得的φ7,重作上述计算,至满意。由于计算Y1=ω1/ω7用有速度分析的计算式,所以,位置分析和速度分析可同步进行。
结果:φ1=60°;φ2=137.7864°;φ3=50.7205°:φ4=97.6755°;φ6=20.7205°;φ7=123.1067°。
速度分析:
由vD=vF+vDF可写出
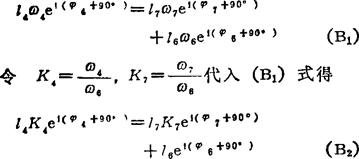
由(B2)式可解得K4、K7,
又由vC=vB+vCB=vD+vCD可写出
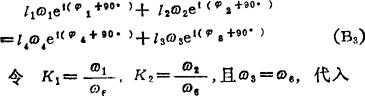
(B3)式得
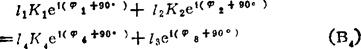
由(B4)式解得K1、K2。于是ω6=ω1/K1,ω2=K2ω6,ω3=ω6,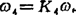 ,ω3=K7ω6。
,ω3=K7ω6。
结果2ω1=10rad/s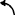 ;ω2=1.1853rad/s
;ω2=1.1853rad/s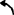 ,ω3=0.9416rad/s
,ω3=0.9416rad/s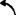 ;ω4=3.5971rad/s
;ω4=3.5971rad/s ;ω6=ω3;ω7=7.6971rad/s
;ω6=ω3;ω7=7.6971rad/s 。
。
加速度分析:
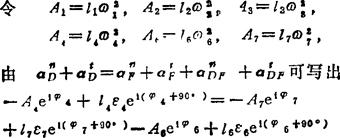
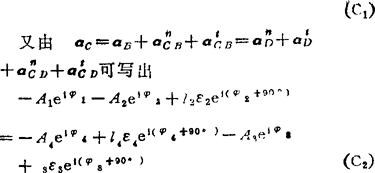
由(C1)、(C2)两式可解得ε2、ε3、ε4、ε7。具体解法如下:
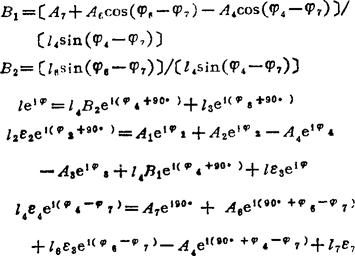
由以上算式和方程的顺序算出B1、B2,解得1、φ、ε2、ε3、ε4、ε7。
结果:ε2=-25.8266rad/s2 ;ε3=8.2552rad/s2
;ε3=8.2552rad/s2 ;ε4=-22.4044rad/s2
;ε4=-22.4044rad/s2 ;ε7=-35.9067rad/s2
;ε7=-35.9067rad/s2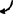 。
。
速度图与加速度图分别如图e)f)所示。其中
图e)为速度图,与(B1)、(B3)式对应;图中pb与机构图中的曲柄AB垂直。图f)为加速度图,与(C1)、(C2)式对应。速度图、加速度图可由计算结果按对应的矢量方程式画出,也可用计算机绘制、屏幕显示。若计算结果有误,则绘制的矢量图不封闭。
例5.3-15~5.3-19的运动线图分别见图5.3-5~5.3-9。
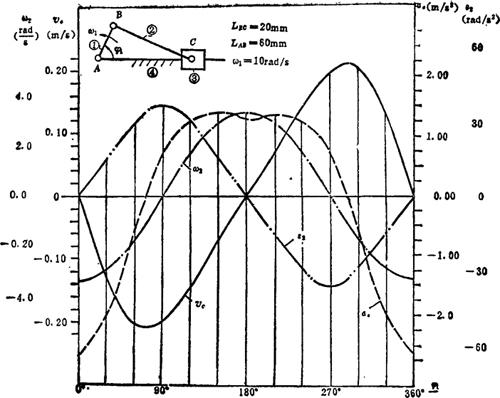
图5.3-5 曲柄滑块机构运动线图
图5.3-6 正切机构运动线图
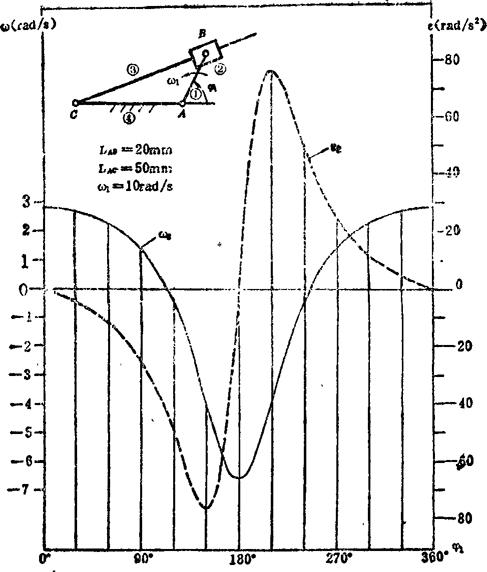
图5.3-7 导杆机构运动线图

图5.3-8 铰链四杆机构运动线图
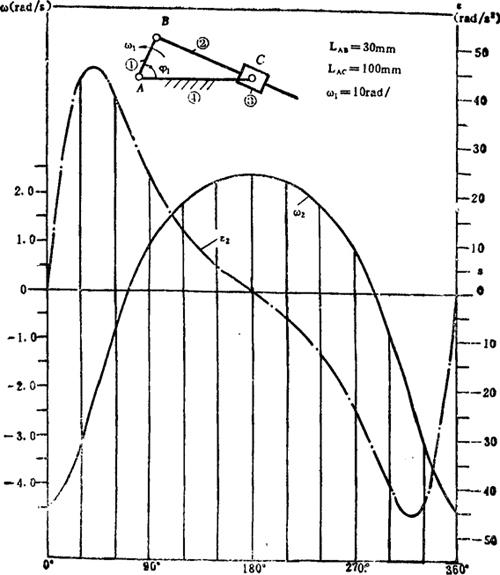
图5.3-9 曲柄摇块机构运动线图