矢量方程图解法

出处：按学科分类—工业技术 北京出版社《现代综合机械设计手册中》第1889页（2943字）

矢量方程图解法：按照相对运动原理列出的速度、、加速度矢量方程，用一定比例尺画出位置图、速度图、加速度图，从图中测量出相应的线段，求出速度、加速度。

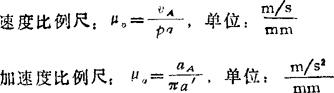
以上式中v_A为A点速度(m／s)；pa为在速度图中表示v_A的线段长度(mm)；a_A为A点加速度(m／s²)；πa′为在加速度图中表示a_A的线段长度(mm)。

设已知机构的各杆长度、主动件位置(φ₁)、主动件角速度ω₁=常数。

例5．3-9 曲柄滑块机构。其矢量方程：

vc= vB+ vcB……(A)

作法：

①选取μ₁，画出位置图a)。

②取v_B=l_ABω₁，方向⊥AB，指向同ω₁一致

③ 取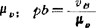，由(A)式画出速度图b)。

④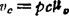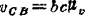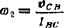；；，单位为rad／s；各速度方向见图。

⑤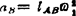，方向∥AB、B→A；=，方向∥BC、C→B。

⑥ 取μ_a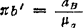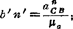；；；由(B)式画出加速度图c)。

⑦ ac=πс′μ_a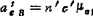；；，单位为rad／s²；各加速度方向见图。

说明：由同一构件的两点列矢量方程，是矢量方程图解法的基本原理之一；本例选构件2的B、C两点列矢量方程，是基于B点是速度、加速度已知的点，而C点是速度方向线、加速度方向线已知的点。

例5．3-10 正切机构。其矢量方程：

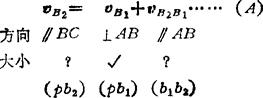
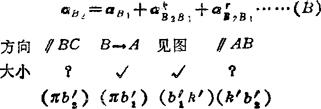
作法：

①选取μ₁，画出位置图a)。

②v_B1=ABμ₁ω₁， 方向⊥AB，指向同ω₁一致。

③ 取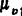；；由(A)式画出速度图b)。

④ vB₂=pb₂×μ_v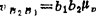；；；ω₂=ω₁；各速度方向见图。

⑤，方向B→A；=2vB₂B1ω₁，指向由vB₂B₁按ω₁方向转90°定，选μa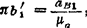；；；由(B)式画出加速度图c)。

⑥；aB₃=aB₂；ε₂=ε₁=0；各加速度方向见图。

说明：当机构中含有组成移动副的两个活动构件时，由这两个构件的重合点列矢量方程，是矢量万程图解法基本原理之二；本例选构件1、2的重合点B₁、B₂列矢量方程，是基于B₁点是速度，加速度已知的点，而B₂点是速度方向线、加速度方向线已知的点。

例5．3-11 摆动导杆机构。其矢量方程：

…………………………(A)

作法：

①选取μ₁；画出位置图a)。

②v_B1=l_ABω₁，方向上AB，指向同ω₁一致；

③ 取μ_v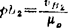；；由(A)式画出速度图b)。

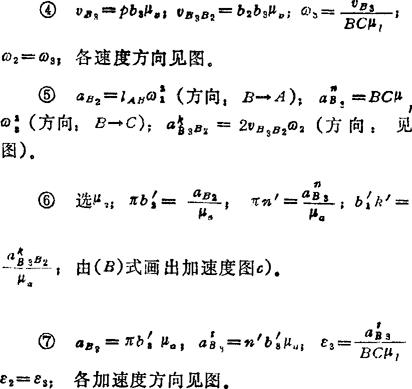
说明：构件2、3组成移动副，选重合点(B₂、B₃)列方程，是由于B₂点是速度、加速度均已知的点；B₃点：v_B3的方向线已知。即，其方向线已知。

例5．3-12 铰链四杆机构。其矢量方程：

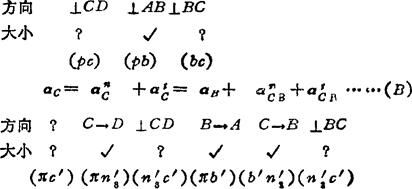
作法：

①选取μ₁；画出位置图a)。

②v_B=l_ABω₁；方向上AB、指向同ω₁一致。

③ 取；；由(A)式画速度图b)。

说明：本例选构件2的B、C两点列方程，是由于B点的v_B、a_B均已知，C点的v_C方向线已知，aC方向线已知。

例5．3-13 曲柄摇块机构。其矢量方程：

v_C，=v_B+vC₂B=vC₃+v_C2c₃……(A)

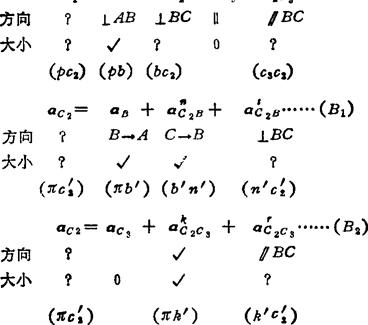
作法：

①选取μ₁，画出位置图a)。

②v_B=_1ABω₁，方向⊥AB，指向同ω₁一致。

③ 取μ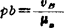_。；；由(A)式画出速度图b)。

例5．3-14 四杆机构。其矢量方程：

作法：

①选取μ₁，画出位置图a)。

②vC₁=ACμ₁ω₁，方向上AC，指向同ω₁一致。

③ 取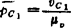；：由(A)式画出速度图b)。

说明：将构件1扩大至包含构件2上的C点是由于：ac₁和ac₁，已知，vc₂和aC₂的方向线已知。